
Calculus is a branch of mathematics considered a gateway to higher-level mathematics. The origins of calculus can be traced to ancient Egypt, where methods involving calculus were used to find the volume of non-standard shapes. Modern calculus has its foundation with the work of Isaac Newton and Gottfried Wilhelm Leibniz in the seventeenth century. Calculus has many applications in physics, economics, and astronomy. Yet the question, “What is Calculus used for?” is still always asked by students.
After completing your internet search regarding the practical application of calculus, take a moment and look around. What math do you see? Where do you recognize the existence of mathematical models?
Notebook

You will benefit from keeping an organized notebook, as this notebook will inform your Learning Log. The Learning Log is an assessment for feedback, but not marks. Choose a notebook format that you prefer, it can be digital or analog (paper notebook.) There will be times where the course will refer to technological options for solving questions and there will be times when you have to complete them on paper, by hand. You will be prompted to reflect on your learning and document evidence of your growth throughout the course.
As you complete the learning activities, you will make use of a notebook of your choice to:
- complete solutions to sample questions and problems;
- define mathematical terms;
- track webpage URLs for practice and information to support your learning;
- reflect on your progress as a self-directed, independent learner.
You will be provided with further instructions at the end of Unit 1 in Learning activity 1.3 on:
- how to prepare your Unit 1: Rates of Change Learning Log Entry
- how to submit this assessment for feedback
Review

In this course, you will be asked to recall concepts you learned in prior mathematics courses. In order to ensure you are prepared with all the necessary skills required for success, it is a good idea to take the time to review.
This first Learning activity will review material from the grade nine mathematics through to the grade twelve functions course.
Expanding Polynomials
Here are some expanding polynomial questions for you to try.
Answers and solutions are available for comparison when you are ready. Please review the solutions to ensure you are following the correct format.
Expand and simplify.
a.
Answer
Solution
b.
Answer
Solution
c.
Answer
Solution
d.
Answer
Solution
Linear Functions
Linear functions are polynomials with a degree of 1. They form straight lines.
The slope/intercept form of a linear function is , where m is the slope and b is the y-intercept.
To determine the equation of a line given the slope and a point on the line use the formula, where m is the slope and is the point on the line.
The slope of a straight line going through and is .
When the slope of a line is positive, we say the line is increasing, which means it goes up from left to right.
Use the view icon to see the increasing movement.
When the slope of a line is negative, we say the line is decreasing, which means it goes down from left to right.
Use the view icon to see the decreasing movement.
A horizontal line has a slope of 0.
The slope of a vertical line is undefined. To understand this better, let’s consider riding a bike. Riding the bike on a flat road there is no slope. When riding the bike up a hill the steepness of the hill is the slope. Now consider a vertical wall. It is impossible to ride the bike straight up the wall. Therefore, the slope is said to be undefined.
Quadratic Functions
Quadratic functions are polynomials with a degree of 2. They form parabolas that open upwards or downwards.
A parabola that opens upwards changes from decreasing to increasing. The change occurs at the vertex.
Use the view icon to see the movement.
A parabola that opens downwards changes from increasing to decreasing. Once again, the change occurs at the vertex.
Use the view icon to see the movement.
Quadratic Formula
The quadratic formula can be used to determine the roots of a quadratic equation in the form .
This method is used when factoring is not possible or is too complicated, but it will work on expressions that can be factored as well.
The quadratic formula:
Example:
Find the roots of . The roots are the intercepts which occur when .
The Factor Theorem
The factor theorem is used to find the roots of polynomial functions with a degree of 3 or higher, such as cubic and quartic functions.
Example: Find the roots of the function
First, use the remainder theorem to find a factor.
Factors will give a remainder of 0.
When ,
Since the remainder is not 0 when , then is not a factor.
When ,
Since the remainder is 0 when , then is a factor.
You can use long division or synthetic division to find the other factors.
Check Your Understanding
Notebook

You can use your notebook to answer the following questions.
Here are some questions for you to try. Answers are available for comparison when you are ready. Please review the solutions to ensure you are following the correct format.
1. Find the equation of a line with slope 5 and passing through the point (-2,4).
The equation of the line is .
; point
use the general equation of the line
The equation of the line is .
2. Factor.
a.
Use factoring by inspection.
Find two numbers that add to 7 and multiply to 12.
The numbers are 3 and 4.
b.
Use factoring by inspection.
Find two numbers that add to -7 and multiply to 10.
The numbers are -5 and -2.
c.
Use factoring by inspection.
Find two numbers that add to -5 and multiply to -24.
The numbers are -8 and 3.
d.
Find two numbers that multiply to -10 and add to 9.
The numbers are -1 and 10.
e.
This is a difference of squares.
The square root of is .
The square root of is .
f.
This is a perfect square.
The square root of is .
The square root of is .
Check the middle term:
3. Find the roots.
a.
The roots are -6 and 4.
b.
There are two possible ways to solve this question:
Method 1: Factoring
The roots are and 2.
Method 2: Quadratic Formula
Or,
The roots are and 2.
c.
This function is not factorable.
Use the quadratic formula.
Or,
The roots are 0.225 and -2.225.
d.
The roots are -1, 2 and -3.
Use the factor theorem.
When ,
Since the remainder is 0 when , then is a factor.
Use long division or synthetic division to find the other factors.
Long Division
The roots are , , .
synthetic division
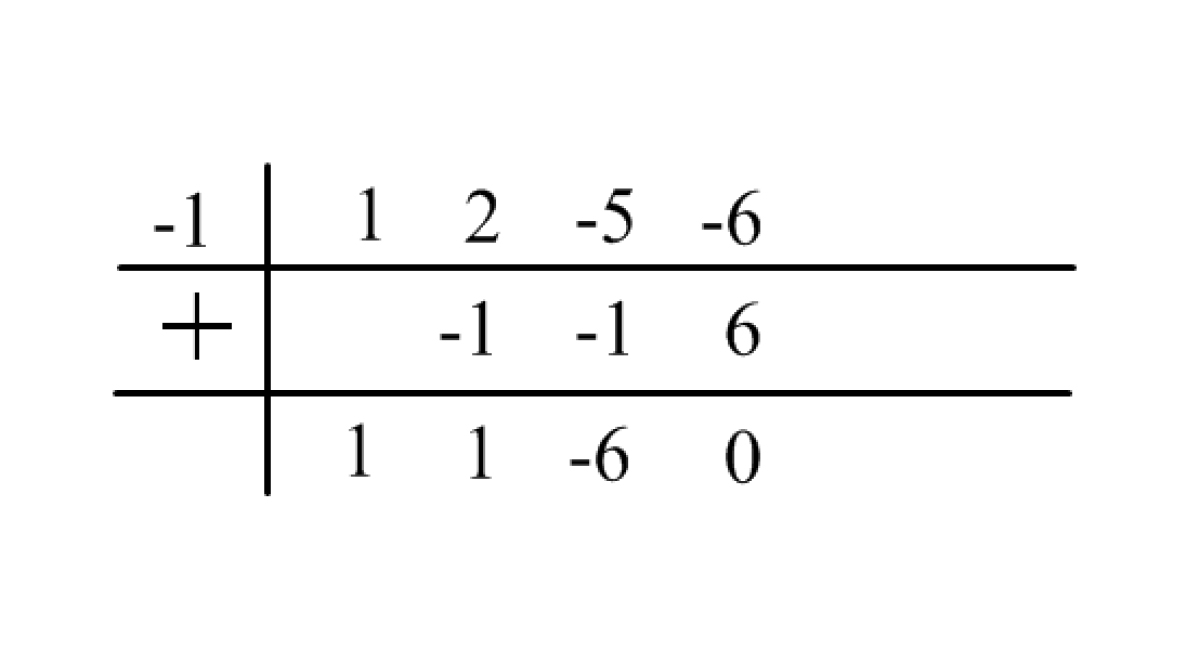
The roots are -1, 2 and -3.
You have now completed Learning activity 1. If you worked through all the examples and Check Your Understanding questions, you should feel comfortable with the prerequisite materials needed for this course:
- expanding and simplifying polynomials;
- determining if a line is increasing or decreasing;
- determining the equation of a line using ;
- determining when a quadratic is increasing or decreasing;
- factoring a polynomial;
- using the quadratic formula to determine the roots of a quadratic equation; and
- using the factor theorem to factor a polynomial with a degree of 3 or higher.
Review the success criteria
Self-Reflection
In this course you are an independent, self-directed learner. Consider this definition of a self-directed learner:

Self-directed learners are aware of how they learn best. They are confident and know when to ask for support. Self-directed learners set goals and make realistic plans to meet those goals. In other words, they make a commitment to their own learning and take responsibility for it.
As a self-directed learner, track your progress on the following:
Rate your understanding on a scale of five to one.
Five means “I have a thorough understanding.” One means “I am confused.”
How confident are you with respect to the following Success Criteria?
You are also encouraged to go online and search for websites that provide worksheets for extra practice. There are also websites that have video demonstrations of a solution to a similar problem.
Here are a couple of suggestions:
University of Waterloo Courseware (Opens in new window)
The Organic Chemistry Tutor (Opens in new window)
Mathwarehouse (Opens in new window)
Kyle Pearce (Opens in new window)
Purplemath (Opens in new window)
You can also contact the Academic Officer.
Feel from to call the Academic Officer from Monday to Friday or email anytime at teacher@tvo.org
When you feel you are ready, you should move on to the Next Steps.
Next Steps
In Learning activity 2, you will begin your Calculus adventure by exploring average rates of change versus instantaneous rates of change.




