Activité d'apprentissage 1.1 : Utilisation des premiers principes pour déterminer l'équation d'une ligne tangente

Le calcul différentiel est une branche des mathématiques considérée comme une porte d’entrée vers les mathématiques de niveau avancé. L’origine du calcul différentiel remonte à l’Égypte antique. À cette époque, on employait des méthodes reposant sur le calcul différentiel pour déterminer le volume de formes non standards. Au XVI^e siècle, les travaux d'Isaac Newton et de Gottfried Wilhelm Leibniz jettent les bases du calcul différentiel moderne. Les applications du calcul différentiel en physique, en économie et en astronomie sont nombreuses. Pourtant, les élèves posent encore la question : « À quoi sert le calcul différentiel? »

Une fois que tu auras terminé tes recherches sur Internet concernant l’application pratique du calcul différentiel, prends quelques instants pour regarder ce qui t’entoure. Quelles mathématiques observes-tu? Où reconnais-tu l’existence de modèles mathématiques?

Réponse de l’élève

Carnet de notes

Tu as avantage à bien organiser ton carnet de notes, car il te servira à remplir ton Carnet d’apprentissage. Le Carnet d'apprentissage est une évaluation en vue d’une rétroaction, mais pas en vue d’une note. Choisis le format que tu préfères pour ton carnet de notes. Il peut être numérique ou sur support papier. Dans le cadre du cours, tu devras parfois utiliser des options technologiques pour résoudre des questions et d’autres fois, tu devras y répondre à la main sur du papier. On te demandera de réfléchir à ton apprentissage et de documenter les preuves de ta progression tout au long du cours.

À mesure que tu réaliseras les activités d’apprentissage, ton carnet de notes te servira :

à résoudre des questions et des problèmes;
à définir les termes mathématiques;
à retrouver l’URL des pages Web sur lesquelles tu peux t’exercer et obtenir de l’information qui facilitera ton apprentissage;
à réfléchir à ta progression en tant qu’apprenante ou apprenant autonome.

On te fournira d’autres instructions dans le cadre de l’activité d’apprentissage 1.3 à la fin de l’Unité 1 pour t’aider :

à préparer ton Unité 1 : Rubrique du Carnet d’apprentissage sur les taux de variation;
à soumettre cette évaluation en vue d’une rétroaction.

Révision

Durant ce cours, tu devras te rappeler les notions que tu as vues dans tes anciens cours de mathématiques. Pour t’assurer d’avoir toutes les compétences nécessaires à ta réussite, on te recommande de prendre le temps de réviser.

Cette première activité d’apprentissage sert à revoir la matière abordée du cours de mathématiques de 9^e année jusqu’au cours de 12^e année sur les fonctions.

Le développement des polynômes

Les fonctions linéaires

Les fonctions quadratiques

La factorisation

La formule quadratique

Le théorème des facteurs

Le développement des polynômes

Voici quelques questions pour t’exercer à développer des polynômes.

Tu peux comparer tes réponses aux réponses et solutions suggérées dès que tu es prêt ou prête. Examine les solutions pour vérifier si tu as utilisé la bonne formule.

Développe et simplifie les expressions suivantes.

a. $(x + 3) (x - 4)$

Réponse de l’élève

Réponse :

$(x + 3) (x - 4) = x^{2} - x - 12$

Solution

$(x + 3) (x - 4) = x^{2} - 4 x + 3 x - 12 = x^{2} - x - 12$

b. $(2 x - 1) (3 x + 5)$

Réponse de l’élève

Réponse :

$(2 x - 1) (3 x + 5) = 6 x^{2} + 7 x - 5$

Solution

$(2 x - 1) (3 x + 5) = 6 x^{2} + 10 x - 3 x - 5 = 6 x^{2} + 7 x - 5$

c. $(3 x - 7) (3 x + 7)$

Réponse de l’élève

Réponse :

$(3 x - 7) (3 x + 7) = 9 x^{2} - 49$

Solution

$(3 x - 7) (3 x + 7) = 9 x^{2} + 21 x - 21 x - 49 = 9 x^{2} - 49$

d. ${(5 x - 2)}^{2}$

Réponse de l’élève

Réponse :

${(5 x - 2)}^{2} = 25 x^{2} - 20 x + 4$

Solution

${(5 x - 2)}^{2} = (5 x - 2) (5 x - 2) = 25 x^{2} - 10 x - 10 x + 4 = 25 x^{2} - 20 x + 4$

Les fonctions linéaires

Les fonctions linéaires sont des polynômes de degré 1. Elles forment des droites.

L’équation sous la forme pente-ordonnée à l’origine d’une fonction linéaire est $y = m x + b$ , où m est la pente de la droite et b, l’ordonnée à l’origine. Cette forme est aussi appelée explicite ou fonctionnelle.

Pour déterminer l’équation d’une droite à partir des données sur la pente et d’un point sur la droite, utilise la formule $y = m (x - x_{1}) + y_{1}$ , où m est la pente et $(x_{1}, y_{1})$ un point sur la droite.

La pente d’une droite qui passe par les points $A (x_{1}, y_{1})$ et $B (x_{2}, y_{2})$ est $m = \frac{y_{2} - y_{1}}{x_{2} - x_{1}}$ .

Quand la pente d’une droite est positive, on qualifie la droite d’ascendante, car elle monte de gauche à droite.

Sers-toi de l'icône d’affichage pour voir le mouvement ascendant.

Quand la pente d’une droite est négative, on qualifie la droite de descendante, car elle descend de gauche à droite.

Sers-toi de l'icône d’affichage pour voir le mouvement descendant.

La pente d’une droite horizontale est de 0.

La pente d’une droite verticale est non définie. Pour t’aider à mieux comprendre, examinons une promenade à vélo. Quand on fait du vélo sur une route plane, il n’y a pas de pente. Si on monte une côte à vélo, le taux de variation de la côte est la pente. Examinons maintenant un mur vertical. Il est impossible de monter directement sur le mur à vélo. On dit donc que la pente est non définie.

Les fonctions quadratiques

Les fonctions quadratiques sont des polynômes de degré 2. Elles forment des paraboles concaves vers le haut ou vers le bas.

Une parabole concave vers le haut passe de décroissante à croissante. Le point où se produit le changement s’appelle le sommet.

Sers-toi de l'icône d’affichage pour voir le mouvement.

Une parabole concave vers le bas passe de croissante à décroissante. Là encore, le changement se produit au sommet.

Sers-toi de l'icône d’affichage pour voir le mouvement.

La factorisation

On peut se servir de la factorisation pour trouver les racines (ou $abscisses à$ l’origine) d’une fonction.

Voici les cinq types de factorisation les plus courants :

La mise en évidence d’un facteur commun

Exemple : $16 x^{2} y^{3} + 24 x^{5} y + 64 x^{6} y^{5} + 8 x^{2} y$

Le facteur commun est $8 x^{2} y$ .

$16 x^{2} y^{3} + 24 x^{5} y + 64 x^{6} y^{5} + 8 x^{2} y = 8 x^{2} y (\frac{16 x^{2} y^{3}}{8 x^{2} y} + \frac{24 x^{5} y}{8 x^{2} y} + \frac{64 x^{6} y^{5}}{8 x^{2} y} + \frac{8 x^{2} y}{8 x^{2} y})$

$= 8 x^{2} y (2 y^{2} + 3 x^{3} + 8 x^{4} y^{4} + 1)$

La technique du produit-somme

Exemple : $x^{2} + 5 x + 6$

Trouve deux nombres dont le produit est 6 et la somme est 5.

Les nombres sont +2 et +3.

$x^{2} + 5 x + 6 = (x + 2) (x + 3)$

La décomposition de trinômes

Exemple : $2 x^{2} + 7 x - 15$

Trouve deux nombres dont le produit est -30 $(2 \times - 15)$ et dont la somme est 7.

Les nombres sont -3 et +10.

$2 x^{2} + 7 x - 15 = 2 x^{2} - 3 x + 10 x - 15 = x (2 x - 3) + 5 (2 x - 3) = (2 x - 3) (x + 5)$

Tu ne parviens pas à trouver les nombres? Voici une méthode fiable.

Trouve les deux nombres!

Si tu ne parviens pas à trouver les deux nombres en décomposant les trinômes, il existe une méthode efficace fondée sur la moyenne des deux nombres.

Soit $12 x^{2} - 32 x - 35$ , tu dois trouver deux nombres dont la somme est -32 et dont le produit est $12 \times (- 35) = - 420$ .

La moyenne des deux nombres est $\frac{- 32}{2} = - 16$ .

Les deux nombres que tu cherches sont équidistants de -16.

Le plus grand des deux nombres correspond à -16 + h et le plus petit à -16 - h.

$\begin{array}{l} (- 16 + h) (- 16 - h) = - 420 \\ 256 - h^{2} = - 420 \\ 676 = h^{2} \\ 26 = h \end{array}$

Le plus grand des deux nombres est $- 16 + 26 = 10$ et le plus petit est $- 16 - 26 = - 42$

Tu as maintenant les nombres à utiliser pour factoriser par décomposition.

$12 x^{2} + 10 x - 42 x - 35 = 2 x (6 x + 5) - 7 (6 x + 5) = (6 x + 5) (2 x - 7)$

Cette méthode permet d’éviter les essais systématiques et est toujours fiable.

La différence de carrés

Exemple : $16 x^{2} - 25 y^{2}$

La racine carrée de $16 x^{2}$ est $4 x$ .

La racine carrée de $25 y^{2}$ est $5 y$ .

$16 x^{2} - 25 y^{2} = (4 x + 5 y) (4 x - 5 y)$

Le trinôme carré parfait

Exemple : $144 x^{2} + 312 x + 169$

La racine carrée de $144 x^{2}$ est $12 x$ .

La racine carrée de $169$ est $13$ .

Examine le terme central : $2 \times 12 x \times 13 = 312 x$

$144 x^{2} + 312 x + 169 = (12 x + 13)^{2}$

La formule quadratique

On peut se servir de la formule quadratique pour déterminer les racines d’une équation quadratique de la forme $y = a x^{2} + b x + c$ .

Cette méthode est employée quand la factorisation est impossible ou trop complexe, mais on peut aussi l’appliquer aux expressions factorisables.

La formule quadratique : $x = \frac{- b \pm \sqrt{b^{2} - 4 a c}}{2 a}$

Exemple :

Trouve les racines de $y = 4 x^{2} - 4 x - 8$ . Les racines sont les $abscisses à$ l’origine obtenues quand $y = 0$ .

Étape 1
Étape 2

Étape 1 :

a = 4; b = -4; c = -8

$x = \frac{- b \pm \sqrt{b^{2} - 4 a c}}{2 a} x = \frac{- (- 4) \pm \sqrt{(- 4)^{2} - 4 (4) (- 8)}}{2 (4)} x = \frac{4 \pm \sqrt{16 + 128}}{8} x = \frac{4 \pm \sqrt{144}}{8} x = \frac{4 \pm 12}{8}$

Étape 2 :

$x = \frac{4 + 12}{8} x = \frac{16}{8} x = 2$

Ou,

$x = \frac{4 - 12}{8} x = \frac{- 8}{8} x = - 1$

Les racines de $y = 4 x^{2} - 4 x - 8$ sont 2 et -1.

Le théorème des facteurs

On se sert du théorème des facteurs pour trouver les racines de fonctions polynomiales ayant un degré supérieur ou égal à 3, comme les fonctions cubiques ou quartiques.

Exemple : Trouve les racines de la fonction définie par l’équation $y = x^{3} - 7 x - 6$

Tout d’abord, utilise le théorème du reste pour trouver un facteur.

Avec les facteurs, tu obtiendras un reste de 0.

Quand $x = 1$ , $y = (1)^{3} - 7 (1) - 6 = - 12$

Puisque le reste n’égale pas 0 quand $x = 1$ , alors $(x - 1)$ n’est pas un facteur.

Quand $x = - 1$ , $y = (- 1)^{3} - 7 (- 1) - 6 = 0$

Puisque le reste est de 0 quand $x = - 1$ , alors $(x + 1)$ est un facteur.

Tu peux faire une division longue ou une division synthétique pour trouver les autres facteurs.

Méthode de la division longue :

Méthode de la division synthétique :

Une droite horizontale portant la mention -16 comporte trois points. Il y en a un à chaque extrémité et un au milieu. Les deux segments de la droite ont la même longueur. Au-dessus de chaque segment d’égale longueur de la droite se trouve une ligne munie d’une flèche à son extrémité désignée par la lettre h.

Les racines sont -1, -2 et 3.

$x^{3} - 7 x - 6 = (x + 1) (x^{2} - x - 6) = (x + 1) (x + 2) (x - 3)$

Carnet de notes

Réponds aux questions suivantes en te servant de ton carnet de notes.

Vérifie ta compréhension

À toi de jouer!

Voici quelques questions pour t’exercer. Tu peux comparer tes réponses aux réponses suggérées dès que tu es prêt ou prête. Examine les solutions pour vérifier si tu as utilisé la bonne formule.

1. Trouve l’équation d'une droite ayant une pente de 5 et qui passe par le point (-2, 4).

L'équation de la droite est $y = 5 x + 14$ .

$m = 5$ ; point $(- 2, 4)$

Utilise la forme générale de l’équation de la droite $y = m (x - x_{1}) + y_{1}$

$y = m (x - x_{1}) + y_{1} y = 5 (x - (- 2)) + 4 y = 5 (x + 2) + 4 y = 5 x + 10 + 4 y = 5 x + 14$

L'équation de la droite est $y = 5 x + 14$ .

2. Factorise.

a. $x^{2} + 7 x + 12$

Utilise la technique du produit-somme.

Trouve deux nombres dont la somme est 7 et dont le produit est 12.

Les nombres sont 3 et 4.

$x^{2} + 7 x + 12 = (x + 3) (x + 4)$

b. $x^{2} - 7 x + 10$

Utilise la technique du produit-somme.

Trouve deux nombres dont la somme est -7 et dont le produit est 10.

Les nombres sont -5 et -2.

$x^{2} - 7 x + 10 = (x - 5) (x - 2)$

c. $x^{2} - 5 x - 24$

Utilise la technique du produit-somme.

Trouve deux nombres dont la somme est -5 et dont le produit est -24.

Les nombres sont -8 et 3.

$x^{2} - 5 x - 24 = (x - 8) (x + 3)$

d. $2 x^{2} + 9 x - 5$

Trouve deux nombres dont le produit est -10 et la somme est 9.

Les nombres sont -1 et 10.

$2 x^{2} + 9 x - 5 = 2 x^{2} - 1 x + 10 x - 5 = x (2 x - 1) + 5 (2 x - 1) = (2 x - 1) (x + 5)$

e. $49 x^{2} - 36 y^{2}$

Il s’agit d’une différence de carrés.

La racine carrée de $49 x^{2}$ est $7 x$ .

La racine carrée de $36 y^{2}$ est $6 y$ .

$49 x^{2} - 36 y^{2} = (7 x + 6 y) (7 x - 6 y)$

f. $64 x^{2} - 80 x + 25$

Il s’agit d’un trinôme carré parfait.

La racine carrée de $64 x^{2}$ est $8 x$ .

La racine carrée de $25$ est $5$ .

Examine le terme central : $2 \times 8 x \times 5 = 80 x$

$64 x^{2} - 80 x + 25 = (8 x - 5)^{2}$

3. Trouve les racines.

a. $y = x^{2} + 2 x - 24$

$\begin{array}{l} y = x^{2} + 2 x - 24 \\ y = (x + 6) (x - 4) \end{array}$

Les racines sont -6 et 4.

b. $y = 3 x^{2} - 5 x - 2$

Tu peux employer l’une ou l’autre des méthodes suivantes pour résoudre la question :

Méthode 1
Méthode 2

Méthode 1 : La factorisation

$\begin{array}{l} y = 3 x^{3} - 5 x - 2 \\ y = (3 x + 1) (x - 2) \end{array}$

Les racines sont $- \frac{1}{3}$ et 2.

Méthode 2 : La formule quadratique

$a = 3; b = - 5; c = - 2 = \frac{- b \pm \sqrt{b^{2} - 4 a c}}{2 a} x = \frac{- (- 5) \pm \sqrt{(- 5)^{2} - 4 (3) (- 2)}}{2 (3)} x = \frac{5 \pm \sqrt{25 + 24}}{6} x = \frac{5 \pm \sqrt{49}}{6} x = \frac{5 \pm 7}{6}$

$x = \frac{5 + 7}{6} x = \frac{12}{6} x = 2$

Ou,

$x = \frac{5 - 7}{6} x = \frac{- 2}{6} x = - \frac{1}{3}$

Les racines sont $- \frac{1}{3}$ et 2.

c. $y = 2 x^{2} + 4 x - 1$

Cette fonction n'est pas factorisable.

Utilise la formule quadratique. $a = 2; b = 4; c = - 1 = \frac{- b \pm \sqrt{b^{2} - 4 a c}}{2 a} x = \frac{- 4 \pm \sqrt{(4)^{2} - 4 (2) (- 1)}}{2 (2)} x = \frac{- 4 \pm \sqrt{16 + 8}}{4} x = \frac{- 4 \pm \sqrt{24}}{4}$

$x = \frac{- 4 \pm 4,9}{4}$

$\begin{array}{l} x = \frac{- 4 + 4,9}{4} \\ x = \frac{0,9}{4} \end{array}$

$x = 0,225$

Ou,

$x = \frac{- 4 - 4,9}{4}$

$\begin{array}{l} x = \frac{- 8,9}{4} \\ x = - 2,225 \end{array}$

Les racines sont 0,225 et -2,225.

d. $y = x^{3} + 2 x^{2} - 5 x - 6$

Les racines sont -1, 2 et -3.

Utilise le théorème des facteurs.

Quand $x = - 1$ , $y = (- 1)^{3} + 2 (- 1)^{2} - 5 (- 1) - 6 = 0$

Puisque le reste est de 0 quand $x = - 1$ , alors $(x + 1)$ est un facteur.

Utilise la division longue ou la division synthétique pour trouver les autres facteurs.

Division longue
Division synthétique

Division longue

Division synthétique

$y = x^{3} + 2 x^{2} - 5 x - 6 y = (x + 1) (x^{2} + x - 6) y = (x + 1) (x - 2) (x + 3)$

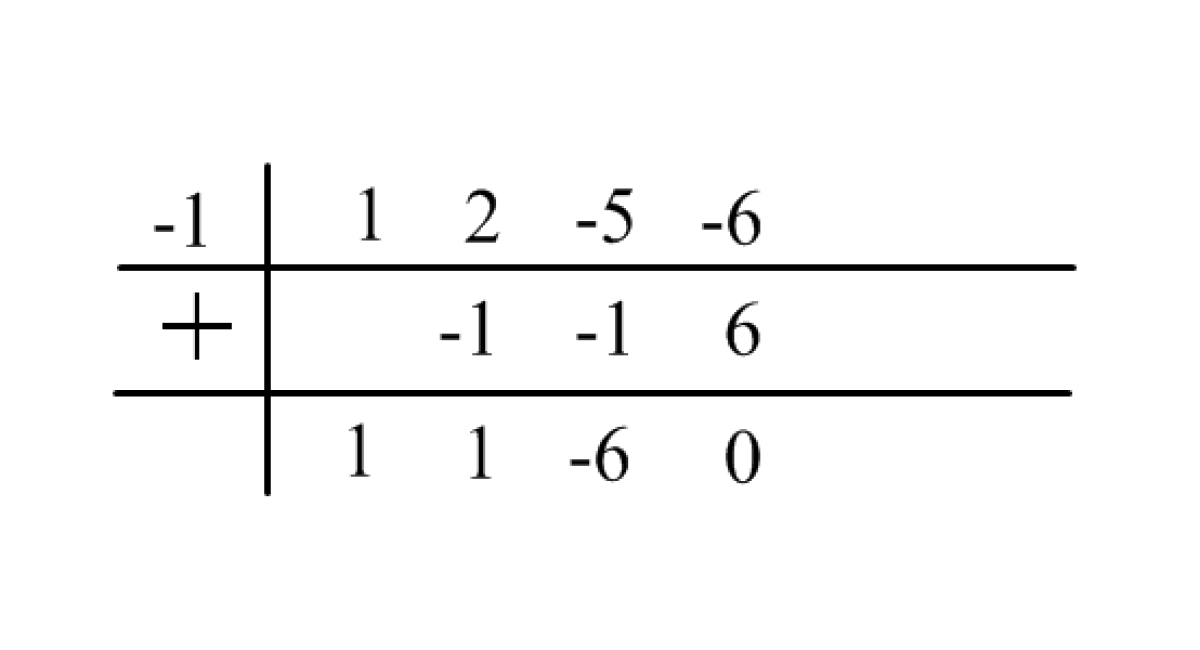
Les racines sont -1, 2 et -3.

Tu as maintenant terminé l’activité d’apprentissage 1. Si tu as fait tous les exemples de problèmes et répondu aux questions servant à vérifier ta compréhension, tu devrais maîtriser les compétences préalables requises pour ce cours :

développer et simplifier des polynômes;
déterminer si une droite est ascendante ou descendante;
déterminer l’équation d’une droite à l’aide de $y = m x + b$ ;
déterminer si une fonction quadratique est croissante ou décroissante;
factoriser un polynôme;
utiliser la formule quadratique pour déterminer les racines de l’équation quadratique;
utiliser le théorème des facteurs pour factoriser un polynôme ayant un degré supérieur ou égal à 3.

Passe en revue les critères de réussite

Réflexion personnelle

Dans le cadre de ce cours, tu es une apprenante ou un apprenant autonome. Lis attentivement cette définition d’un apprenant autonome :

Les apprenants autonomes connaissent les modes d’apprentissage qui leur conviennent le mieux. Ils ont confiance en eux et savent quand demander du soutien. Les apprenants autonomes se fixent des objectifs et adoptent des plans réalistes pour les atteindre. Autrement dit, ils assument la responsabilité de leur propre apprentissage et s’engagent à cet égard.

En tant qu’apprenante ou apprenant autonome, évalue ta progression en fonction des énoncés ci-dessous :

Accorde-toi une note d’un à cinq.

Cinq signifie « Ma compréhension est excellente ». Un signifie « Je n’arrive pas à comprendre ».

Énoncé	Pas du tout d’accord	En désaccord	D’accord	Tout à fait d’accord
Je sais quels modes d'apprentissage me conviennent le mieux	1	2	3	4
J’ai confiance en mes capacités d’apprenante ou apprenant	1	2	3	4
Je sais quand, où et à qui demander du soutien	1	2	3	4
J’assume la responsabilité de mon propre apprentissage et m’engage à cet égard	1	2	3	4
Je m’exerce à appliquer de nouvelles compétences dans le but de m’améliorer	1	2	3	4
Je réfléchis à mon propre apprentissage pour déterminer mes points forts et ceux que je peux améliorer	1	2	3	4
Je me sers de la rétroaction pour m’améliorer	1	2	3	4

Maintenant, prends quelques instants pour passer en revue les objectifs d’apprentissage et critères de réussite de cette activité d’apprentissage et y réfléchir.

Comment évaluerais-tu ta compréhension des concepts abordés pendant cette activité d'activité d’apprentissage? Choisis l’une de ces quatre réponses.

J’estime avoir une excellente compréhension des concepts.

Formidable! Félicitations! Tu peux maintenant passer aux prochaines étapes.

J’estime avoir une très bonne compréhension des concepts.

C’est super! Quel concept te pose le plus problème? On t’invite à te rendre en ligne et à trouver des sites Web qui proposent des exercices supplémentaires. De plus, certains sites Web comprennent des démonstrations vidéo illustrant la solution de problèmes similaires à ceux vus durant cette unité.

J’estime avoir une bonne compréhension des concepts.

Trouves-tu que ces concepts sont trop difficiles à comprendre en général ou penses-tu pouvoir travailler à t’améliorer?

Si tu crois pouvoir travailler à améliorer ta compréhension, tu devrais réviser de nouveau les exemples et les exercices. Tu devrais aussi répondre de nouveau aux questions qui servent à vérifier ta compréhension.

J’estime avoir une compréhension limitée des concepts.

Trouves-tu que ces concepts sont trop difficiles à comprendre en général ou penses-tu pouvoir travailler à t’améliorer?

Selon toi, à quel point maîtrises-tu les critères de réussite suivants?

Énoncé	J’ai besoin d’aide	Je suis sur la bonne voie	Je suis capable
Développer et simplifier des polynômes	1	2	3
Déterminer si une droite est ascendante ou descendante	1	2	3
Déterminer l’équation d’une droite à l’aide de $y = m x + b$	1	2	3
Déterminer si une fonction quadratique est croissante ou décroissante	1	2	3
Factoriser un polynôme	1	2	3
Utiliser la formule quadratique pour déterminer les racines de l’équation quadratique	1	2	3
Utiliser le théorème des facteurs pour factoriser un polynôme ayant un degré supérieur ou égal à 3	1	2	3

On t’invite également à te rendre en ligne et à trouver des sites Web qui proposent des feuilles de travail, pour t'exercer davantage. De plus, certains sites Web comprennent des démonstrations vidéo illustrant la solution de problèmes similaires à ceux vus durant cette unité.

En voici quelques-uns :

« Répertoire de révision - mathématiques - 5e secondaire – TS » (s’ouvrira dans une nouvelle fenêtre)

« Mathéma-TIC » (s’ouvrira dans une nouvelle fenêtre)

« Idéllo TFO Dossier thématique : Mathématiques de 9e à 12e année » (s’ouvrira dans une nouvelle fenêtre)

« Central des maths » (s’ouvrira dans une nouvelle fenêtre)

« L’informatique et les math au lycée » (s’ouvrira dans une nouvelle fenêtre)

« Yvan Monka » (s’ouvrira dans une nouvelle fenêtre)

« Swisslearn » (s’ouvrira dans une nouvelle fenêtre)

« Maths en ligne » (s’ouvrira dans une nouvelle fenêtre)

Tu peux aussi communiquer avec le ou la responsable de l’enseignement.

N’hésite pas à l’appeler du lundi au vendredi ou à lui envoyer un courriel à teacher@tvo.org à tout moment.

Passe aux prochaines étapes dès que tu te sentiras prêt ou prête.

Prochaines étapes

Dans le cadre de l’activité d’apprentissage 2, tu te lanceras dans l’étude du calcul différentiel, en examinant les caractéristiques des taux de variation moyens et des taux de variation instantanés.

Remerciements

Objectifs d’apprentissage

Critères de réussite

Carnet de notes

Révision

Le développement des polynômes

Les fonctions linéaires

Les fonctions quadratiques

La factorisation

La formule quadratique

Le théorème des facteurs

Le développement des polynômes

Les fonctions linéaires

Les fonctions quadratiques

La factorisation

La mise en évidence d’un facteur commun

La technique du produit-somme

La décomposition de trinômes

La différence de carrés

Le trinôme carré parfait

La formule quadratique

Le théorème des facteurs

Méthode de la division longue :

Méthode de la division synthétique :

Carnet de notes

Vérifie ta compréhension

À toi de jouer!

Passe en revue les critères de réussite

Réflexion personnelle

J’estime avoir une excellente compréhension des concepts.

J’estime avoir une très bonne compréhension des concepts.

J’estime avoir une bonne compréhension des concepts.

J’estime avoir une compréhension limitée des concepts.

Prochaines étapes