Similar Figures

Similar figures occur very often in the world around us. Examine the three images of the same boat. The images are the same shape, so they are similar figures. We will get into a more specific definition in a bit. The biggest boat picture is twice as long and twice as high as the bottom images. A photo enlargement will always create a similar figure to the original photo.

If we compare all three pictures, even though one is the reverse image of the other, they are all similar figures. Similar figures can also be the same size; they don’t have to be larger than the others.

Similar Triangles

Definition:

Similar triangles are triangles that are the same shape. There are two geometric relationships (between angles and sides) that make them similar. Below we will find two triangles that illustrate the concept of similarity between triangles. Please note that the angles and sides listed in the diagrams are for explanation purposes only. Triangles don’t have to have 30°, 45° and 105° angles to be similar or have these specific side lengths.

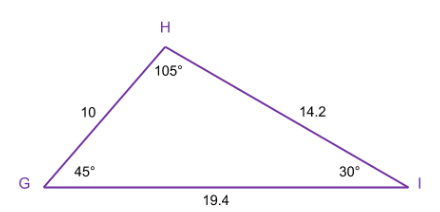
ΔABC ~ ΔGHI is how you write mathematically that ΔABC is similar to ΔGHI. This is called the similarity relationship.

Similar triangles are the same shape. This means that every angle in one triangle has an equal corresponding angle in the second triangle.

Equal angle pairs:

∠ A = ∠ G

∠ B = ∠ H

∠ C = ∠ I

You will often use ratios of sides to show triangles are similar, but before we get into that, a little more about angles.

If two triangles have two pairs of equal angles, then the third in each must also be the same (since the three angles always add to 180°).

So, as soon as you notice two triangles with two equal pairs of angles, then the triangles must be similar. This justification is often called Angle-Angle Similarity, or simply, AA. You can use the acronym AA when explaining why two triangles are similar, assuming the triangles have two pairs of equal angles.

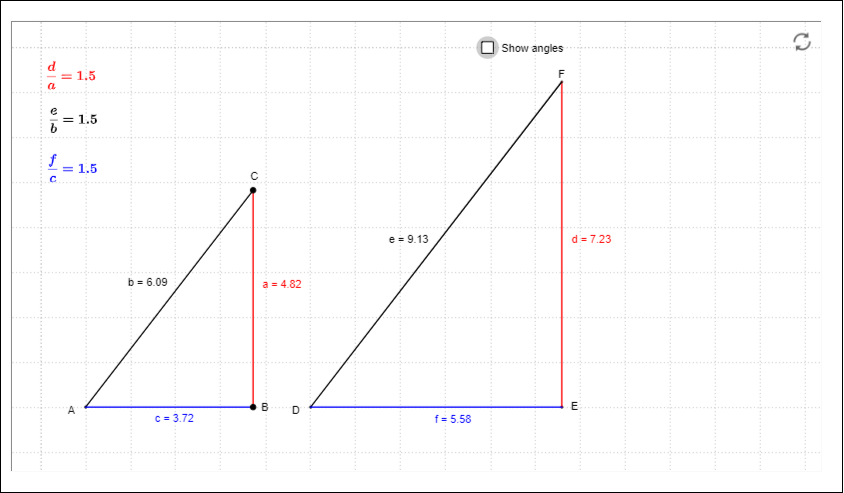
The ratios of the corresponding sides are constant. This means that if we divide a side length from one triangle by its corresponding side in the other triangle, that ratio will be the same for all three pairs of sides.

Relationship between sides:

In $∆ABC and ∆GHI$

$\angle A=\angle G$ . The side across from $\angle A$ is $BC$. The side across from $\angle G$ is $HI$. So, $BC$ is said to correspond to $HI$. In the same way, $\angle B=\angle H$, so $AC$ corresponds to $GI$ and since $\angle C=\angle I$ then $AB$ corresponds to $GH$.

Let’s look at the ratios of the corresponding sides.

$\frac{AB}{GH}= \frac{5}{10}= \frac{1}{2}$

$\frac{BC}{HI}= \frac{7.1}{14.2 }= \frac{1}{2}$

$\frac{AC}{GI}= \frac{9.7}{19.4}= \frac{1}{2}$

Since all three ratios equal $\mathrm{½}$, we write $\frac{AB}{GH}$= $\frac{BC}{HI}$ = $\frac{AC}{GI}$

These are the ratios of the corresponding sides.

For example, if $GH=2\times AB$, then $HI=2\times BC$ and $GI=2\times AC$

It doesn’t matter which triangle has the sides on the top or bottom of these ratios. We could have written the following instead: $\frac{GH}{AB}$ = $\frac{HI}{BC}$ = $\frac{GI}{AC}$ Since the larger sides are in the numerator, the ratio would be $\frac{2}{1}$ or $\frac{GH}{AB}= \frac{HI}{BC}= \frac{GI}{AC }= \frac{2}{1}$

The order the similarity statement is written is important.

In the similarity statement above $A$ and $B$ are first & second, so are $G$ and $H$ so $AB$ corresponds to $GH$.

In the similarity statement above $B$ and $C$ are second & third, so are $H$ and $I$ so $BC$ corresponds to $HI$.

In the similarity statement above $A$ and $C$ are first & third, so are $G$ and $I$ so $AC$ corresponds to $GI$.

Relationship between sides:

$\frac{AB}{GH}= \frac{BC}{HI}= \frac{AC}{GI}$

Or

$\frac{GH}{AB}= \frac{HI}{BC}= \frac{GI}{AC}$

Explore these similar triangles by changing the side lengths and angles. Put your curser on C or B on the first triangle and change the length and angle of the triangle by moving that point. The two things you should pay close attention to are the matching angles and the ratios of the corresponding sides.

Check your understanding.

This is an assessment for learning (not for marks):

Use the diagram representing $\Delta BCD$ and $\Delta FMJ$, to answer the following questions.

Throughout the course you should make a conscious effort to use the formula sheetOpens in a new window that you will be made available to you when you write your final exam.

Here are a few practice exercises you can try in your math journal. Solutions are included for each question.