Bienvenue à l’activité Exploration des triangles semblables ! Non seulement la connaissance des triangles semblables constitue une aptitude mathématique essentielle, mais elle comporte aussi plusieurs applications pratiques. Dans la vie courante, ta connaissance des triangles semblables est mise à profit tous les jours lorsque tu analyses l’architecture d’une structure, les ponts ou la longueur des ombres, ou que tu établis l’angle adéquat selon lequel balancer une batte de baseball.

Plusieurs élèves essaient de maîtriser les mathématiques de niveau secondaire en s’efforçant de mémoriser encore et encore. Il y a bien sûr des choses que tu dois mémoriser, comme les tables de multiplication, mais tu auras plus de succès si tu réfléchis à tes apprentissages et que tu établis des liens entre les sujets. Commençons !

Grille d’évaluation

Prends connaissance de la grille d’évaluation ci-dessous pour t’assurer de bien comprendre les lignes directrices de l’évaluation.

Figures semblables

Les figures semblables sont monnaie courante dans le monde qui nous entoure. Examine ces deux images d’un bateau.  Les deux images du haut ont la même forme, donc il s’agit de figures semblables. Nous découvrirons bientôt une définition plus précise.  L’image du haut est deux fois plus longue et deux fois plus haute que celle du bas. L’agrandissement d’une photo créera toujours une figure semblable à celle de la photo originale.

Si l’on compare ces trois images, ce sont toutes des figures semblables, même si l’une est l’image inverse de l’autre.  Les figures semblables peuvent également être de la même taille; il n’est pas nécessaire que l’autre soit plus grande que l’autre.

Triangles semblables

Définition :

Les triangles semblables sont des triangles qui ont la même forme. Deux relations géométriques (entre les angles et entre les côtés) les rendent semblables. Tu trouveras ci-dessous deux triangles qui illustrent le concept de similitude entre les triangles. Souviens-toi que les angles et les côtés indiqués sur les diagrammes ne sont fournis qu’à titre d’explication. Il n’est pas nécessaire que les triangles affichent des angles de 30°, de 45  et de 105° pour être semblables, ou d’avoir des côtés de longueurs précises.

ΔABC ~ ΔGHI désigne la manière d’indiquer de façon mathématique que le ΔABC est semblable au ΔGHI. C’est ce qu’on appelle une relation de similitude.

Les triangles semblables présentent la même forme. Cela signifie que chaque angle d’un triangle a un angle égal correspondant dans le second triangle.

Paires d’angles égaux :

∠ A = ∠ G

∠ B = ∠ H

∠ C = ∠ I

Vous utiliserez souvent les rapports des côtés pour montrer que les triangles sont similaires, mais avant d'entrer dans le vif du sujet, il faut en savoir un peu plus sur les angles.

Si deux triangles ont deux paires d'angles égaux, alors le troisième dans chacun d'eux doit également être le même (puisque les trois angles s'additionnent toujours à 180°).

Donc, dès que vous voyez deux triangles avec deux paires d'angles égaux, alors les triangles doivent être similaires. Cette justification est souvent appelée Similarité Angle-Angle, ou simplement, AA. Vous pouvez utiliser l'acronyme AA pour expliquer pourquoi deux triangles sont similaires, en supposant que les triangles ont deux paires d'angles égaux.

Les rapports des côtés correspondants sont constants. Cela signifie que si nous divisons la longueur d'un côté d'un triangle par son côté correspondant dans l'autre triangle, ce rapport sera le même pour les trois paires de côtés.

Relations entre les côtés :

Dans ΔABC et ΔGHI

∆ABC et ∆GHI ∠A=∠G∠. Le côté en face de ∠A est BC. Le côté en face de ∠G est HI. Donc, on dit que BC correspond à HI. De la même manière, ∠B=∠H∠, donc AC correspond à GI et comme ∠C=∠I alors AB correspond à GH.

Examinons les ratios des côtés correspondants.

$\frac{AB}{GH}= \frac{5}{10}= \frac{1}{2}$

$\frac{BC}{HI}= \frac{7.1}{14.2 }= \frac{1}{2}$

$\frac{AC}{GI}= \frac{9.7}{19.4}= \frac{1}{2}$

Puisque les trois ratios sont égaux ½ nous écrivons $\frac{AB}{GH}$= $\frac{BC}{HI}$ = $\frac{AC}{GI}$

Ce sont les ratios des côtés correspondants.

Par exemple, si $GH=2\times AB$, le $HI=2\times BC$ et $GI=2\times AC$

Peu importe le triangle dont les côtés se trouvent en haut ou en bas de ces rapports. Nous aurions pu écrire ce qui suit à la place : $\frac{GH}{AB}$ = $\frac{HI}{BC}$ = $\frac{GI}{AC}$. Comme les grands côtés sont au numérateur, le rapport serait de $\frac{2}{1}$ or $\frac{GH}{AB}= \frac{HI}{BC}= \frac{GI}{AC }= \frac{2}{1}$

L'ordre dans lequel la déclaration de similitude est rédigée est important.

Dans la déclaration de similarité ci-dessus, $A$ et $B$ sont les premier et second, tout comme $G$ et $H$ de sorte que $AB$ corresponds à $GH$.

Dans la déclaration de similarité ci-dessus $B$ et $C$ sont premier et troisième, ainsi que $H$ et $I$ de sorte que $BC$ corresponds à $HI$.

Dans la déclaration de similarité ci-dessus $A$ et $C$ asont premier et troisième, ainsi que $G$ et $I$ de sorte que $AC$ corresponds à $GI$.

Relations entre les côtés :

$\frac{AB}{GH}= \frac{BC}{HI}= \frac{AC}{GI}$

Ou

$\frac{GH}{AB}= \frac{HI}{BC}= \frac{GI}{AC}$

Explorez ces triangles similaires en changeant les longueurs et les angles des côtés (Opens in new window). Placez votre curseur sur C ou B dans le premier triangle. Les deux choses auxquelles vous devez prêter attention sont les angles correspondants et les rapports des côtés correspondants.

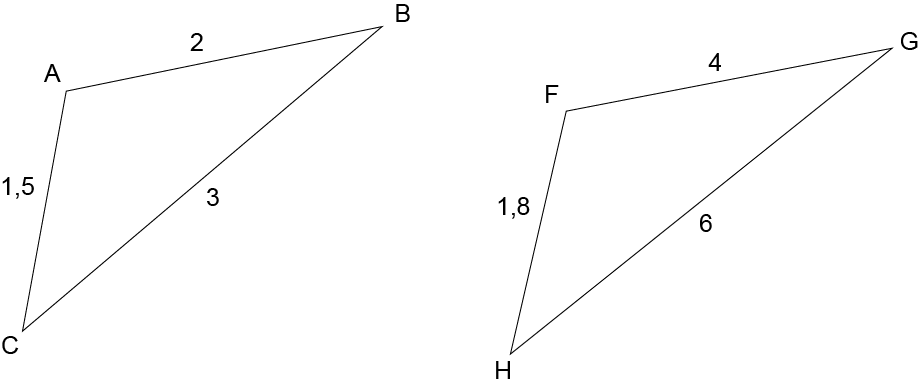
Utilisez le diagramme representant $\Delta BCD$ et $\Delta FMJ$, pour répondre aux questions suivantes.

Tout au long du cours, vous devez faire un effort particulier pour utiliser la feuille de formule s'ouvrira dans une nouvelle fenêtrequi vous sera proposée lors de votre examen final.

Voici quelques exercices pratiques que tu peux essayer. La solution de chaque question est fournie.

Conclusion

Félicitations ! Tu as maintenant terminé l’activité d’apprentissage 1. En ayant travaillé sur tous les exemples tu te sentiras probablement à l’aise pour :

• écrire la relation de similitude entre deux triangles
• établir si des triangles sont semblables ou non

Autovérification

Moment de réflexion ! Prends un moment pour réfléchir à cette activité d’apprentissage.

Quel niveau de confort ci-dessous reflète le mieux ton apprentissage ? Ne t’inquiète pas, tu peux maîtriser définitivement les concepts en repensant les exemples et en pratiquant davantage.

D’accord ou pas d’accord?

Critères de réussite	Je sens que je maîtrise les concepts	Je sens que je suis près de maîtriser les concepts	Je sens que j’ai besoin d’exemples supplémentaires pour maîtriser les concepts	Je sens que je suis loin de maîtriser les concepts
Écrire la relation de similitude entre deux triangles	1	2	2	2
Établir si des triangles sont semblables ou non	1	2	2	2