Types of waves
Take a look at the following pictures:
As you can see in the pictures, there are many different types of waves. Sometimes waves are useful, like water waves when we want to surf, but sometimes they can be destructive, like tsunami waves. Sound waves can help you learn about the environment around you, or give you enjoyment through music, but they can also be destructive when they cause noise pollution or when the sound is so intense that it injures your ear drum.
Use the text box below to write down all the wave types you can think of:
Water waves, waves on a rope, sound waves, light, radio waves, X-rays, microwaves, and many more.
Investigate: Wave on a string
Activity
Now that you have thought about various types of waves, let’s try to understand how a wave is made. In other words, we will try to answer the question: What is a wave?
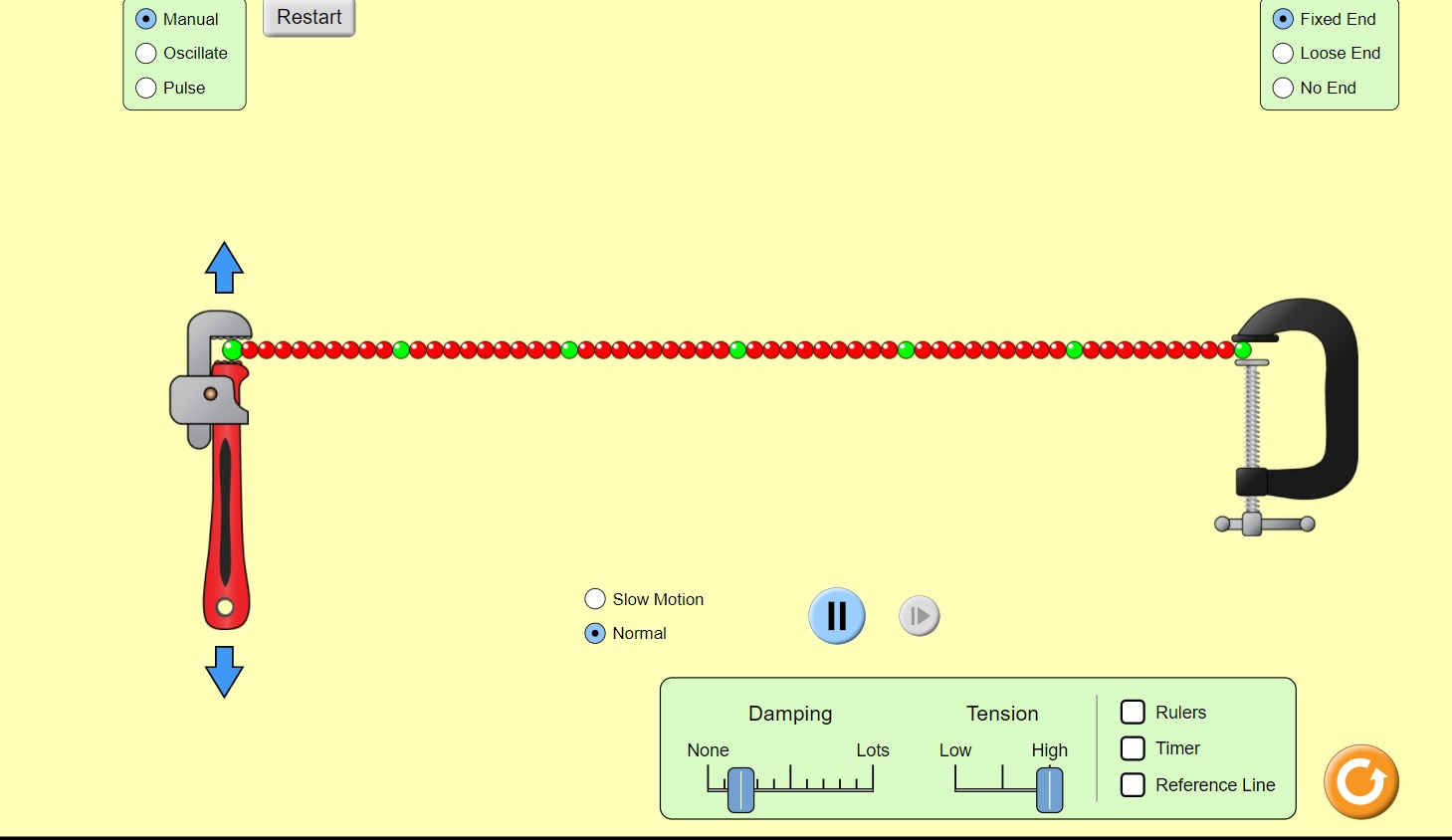
Try the following simulation. You will explore how to make a wave. With the initial settings, try moving the wrench up and down (press and drag) to create waves.
Press Enter here for an accessible version of “Wave on a string.” (Opens in new window)
Describe what you see:
A set of waves is created in the string. The waves stop eventually. They reflect back to their source from the other end as well.
What caused the wave to be made?
You physically had to move one side of the string up and down.
What is a wave?
As the wave travels through the medium, the particles of the medium oscillate or vibrate. That means they move back and forth. In the simulation, the wave travelled through the rope, which is the medium.
A wave, then, is a disturbance that transfers energy from particle to particle along a medium.
A wave is created by a vibration or oscillation of the medium. Think back to the simulation: in order to create the wave or pulse (single wave) you had to move the end of the string up and down.
Examples of waves:

Water wave: Disturbance that transfers through water particles. The medium of the wave is water particles. The water particles oscillate or vibrate as the wave passes through them.

Sound wave: Disturbance that transfers sound energy through air particles. The medium of the sound wave is air particles. The air particles oscillate or vibrate as the sound wave passes through them.
Self-Check: Wave medium
Can you identify the medium in the video?
Rope
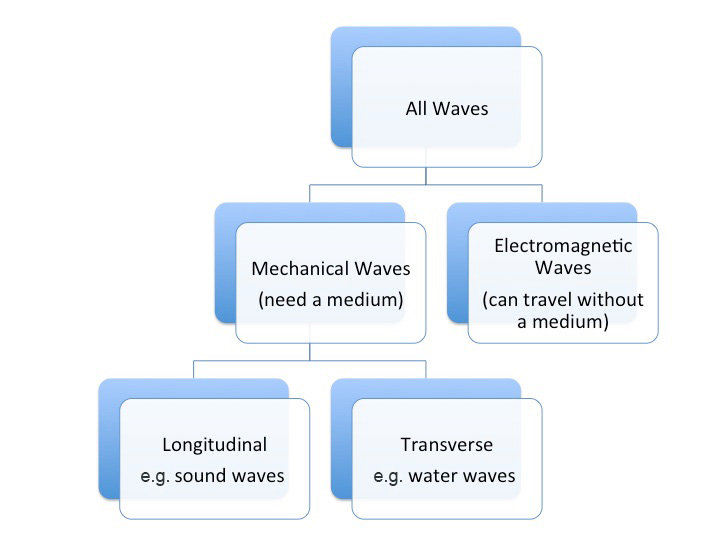
Notice that for the waves to travel in this example, there needs to be a medium. These are examples of mechanical waves.
Classifying waves
Recall that we said waves require a medium. Actually, electromagnetic waves do not require a medium to travel, and can even travel in a vacuum like in outer space. In your physics studies, you will find that we concepts are simplified at first, and then expanded upon.
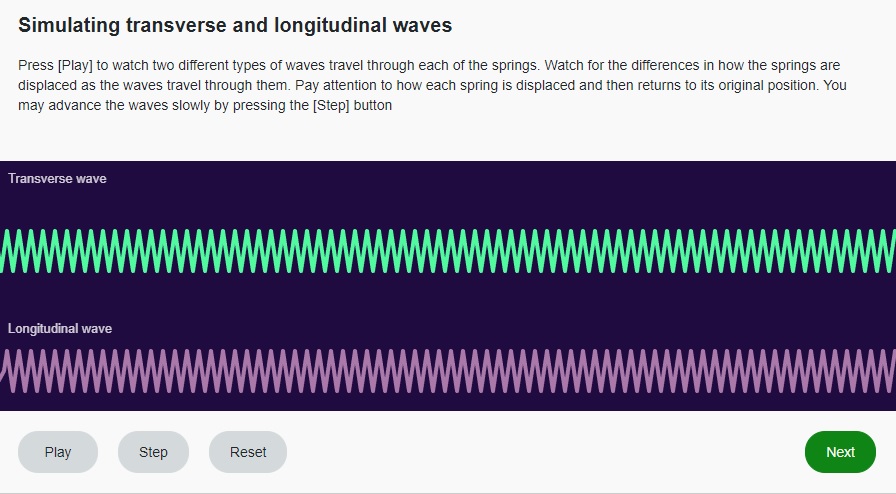
In this learning activity, you will study two types of mechanical waves, longitudinal and transverse, and you will learn how to recognize them. Note that in this course, you will only be learning about mechanical waves.
Transverse waves
In a transverse wave, the motion of the particles and the direction of travel of the energy are at right angles (perpendicular) to each other. Only the energy moves across; the particles remain at their location as they transfer energy from one to the next.
Take a look at the following video to understand the behaviour of a transverse wave:
As you can see, the particles move up and down, but the wave is travelling from right to left, so the energy is moving perpendicular to the motion of the particles.
The figure to the right shows the creation of a transverse wave as the end of a rope is moved through one complete up-and-down cycle, or vibration. Notice that, after completing one cycle, the energy has reached only point E on the rope. The distance the wave has travelled after the source has made one vibration is called a wavelength. This is given the symbol λ (the Greek letter lambda).
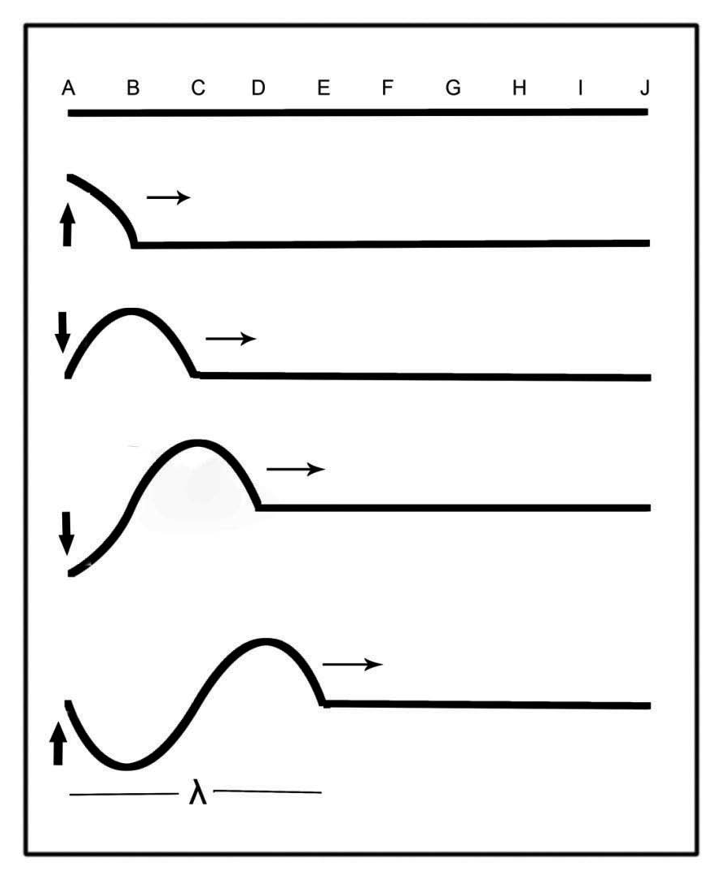
Creation of transverse waves
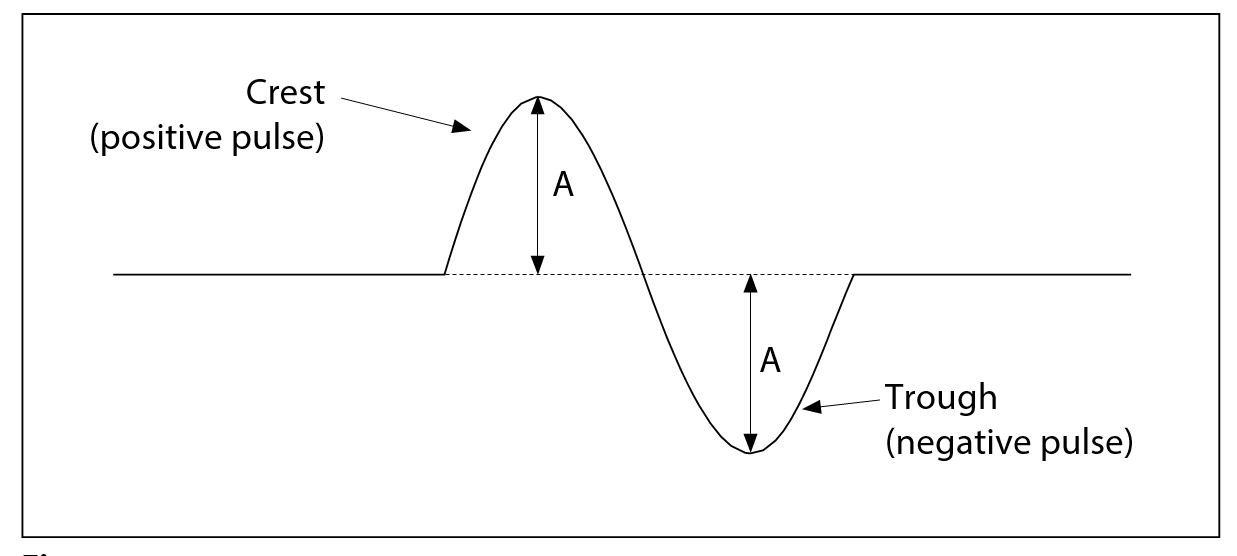
As illustrated in the first figure, the high section of the wave is called a crest and the low section is called a trough. The crest is also called a positive pulse because the amplitude, A, (one half of the vertical distance between crests and troughs) is above the rest position. Troughs are also called negative pulses because their amplitude is below the rest position.
If a periodic vibration is used to produce a transverse wave in a rope, then a series of crests and troughs will be visible in the rope at one time. To produce this type of wave motion, your hand would have to move with a constant frequency up and down, as shown in the second figure. All the crests and troughs would have equal amplitudes and lengths. Notice that the pattern of the waves is repetitive.
The wavelength (the distance across one crest and one trough) remains constant if the period remains constant. It is usually measured in metres or centimetres. Several examples showing how to measure wavelength are shown in the diagram. They are shown by the lines with λ above them.
Transverse waves
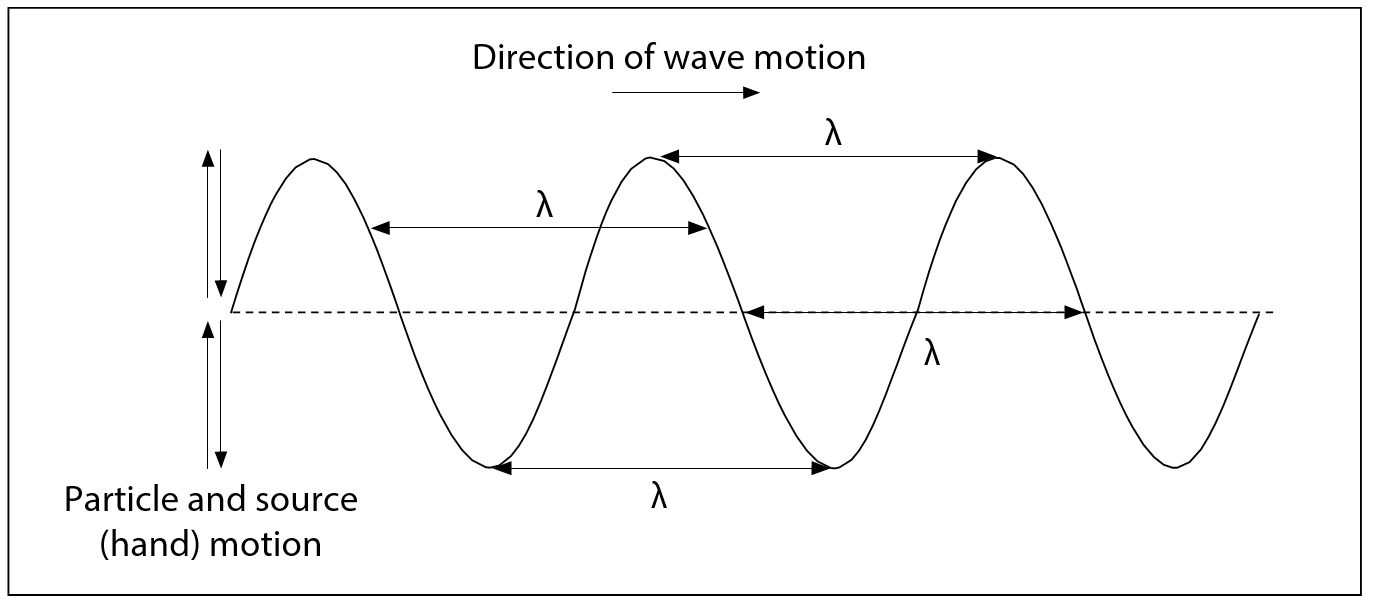
Transverse waves
Longitudinal waves
When the particles in the medium vibrate parallel to the direction of wave motion, the wave is called a longitudinal wave.
Take a look at the following video to understand the behaviour of a longitudinal wave:
The most common longitudinal waves are sound waves. You will learn more about sound waves later in this unit.
One way to visualize longitudinal sound waves is to use a “slinky” spring.

To produce a longitudinal wave in a slinky, arrange it in a straight line on the floor or some other horizontal surface. Tie one end to a fixed position and hold the other end in your hand. With the slinky stretched out to a reasonable length, you can move the end you are holding towards the slinky and then back again, parallel to the length of the slinky. Let’s explore more about longitudinal waves.
This periodic motion will produce compressions in the slinky when you are pushing towards it. In this case, the slinky’s coils will get bunched closer together. You will produce rarefactions when your hand moves away from the slinky. In this case, the coils of the slinky will spread farther apart.
These compressions and rarefactions will move along the length of the slinky, parallel to the direction of wave motion. In general, a compression occurs when the particles of the medium in a longitudinal wave are closer together than normal, and a rarefaction is when the particles are farther apart than normal.
If you tie a ribbon to the slinky, you will see the ribbon move back and forth, parallel to the wave motion, as shown on the right-hand side of the image. For a longitudinal wave, a wavelength is measured from the centres of two successive compressions or rarefactions, as shown in the diagram. As with transverse waves, the maximum displacement of the particles from the rest position is the amplitude. In one cycle, these particles will move a distance of four times the amplitude.

Ideal versus real waves
The previous discussion of waves represents the ideal case. We call them ideal waves (there is no force acting against the wave). However, real waves, such as those in ropes, must pass through the air or rub against a surface, as they move. In such cases, friction often reduces the amplitude of the wave as it moves through the medium. You will also see that the amplitude of the wave gradually decreases as it moves through the medium, but the wavelength does not change.
Activity
Let’s use the wave simulation again. To compare a real wave to an ideal wave, set the damping (on the bottom of the screen) to “None” to mimic an ideal wave. Then, increase the damping to mimic a real wave.
Try this!
Use the "properties of waves" simulation to see the difference between transverse and longitudinal waves made by a spring. Then, answer the questions that follow.
Self-Check: Types of waves
How is a longitudinal wave different from a transverse wave?
In a longitudinal wave, the particles move parallel to the direction of the wave. In a transverse wave, the particles move perpendicular to the direction of the wave.
How would you describe a compression in a longitudinal wave?
It is the part of the wave where the particles are close together.
What is the highest point of a transverse wave called?
The crest.
Look at the following diagram and then answer the question that follows.
In the diagram, what is the distance from E to G in terms of wavelengths?

Half a wavelength.
Periodic motion
Take a look at the following video.
A child moving back and forth on a swing can be described in many of the same ways as wave motion. A playground swing is like a pendulum, which is just a mass tied to a string that is swinging back and forth. Waves are often produced by this type of periodic motion, which is motion that repeats itself over and over again in equally spaced time intervals.
Try this!
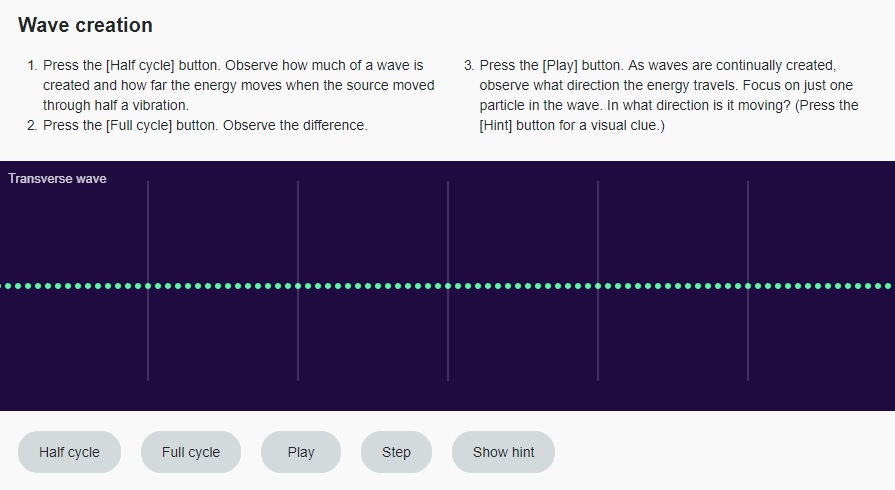
You will have a chance to make your own wave. Follow the instructions in this simulation:
Press Enter here for an accessible version of “Wave creation.” (Opens in new window)
Quantifying wave motion
It is now time to start quantifying wave motion. In other words, you will analyze periodic motion quantitatively (using numbers) rather than just qualitatively (using words) as you have been doing so far in this learning activity.
Before you begin, you will need to review two (2) important concepts in the study of physics: scientific notation and significant figures.
Scientific notation
Scientific notation is used regularly in physics to help us communicate very large numbers (e.g. the mass of the Earth is approximately 6 x 1024 kg), and very small numbers (e.g. the mass of an electron is approximately 9 x 10-31 kg).

The Earth has a mass of 5.98 x 1024 kg.
Need a refresher?
Try the following activity:
Press Enter here for an accessible version of “Scientific notation refresher.” (Opens in new window)
Significant figures
Whenever you do scientific calculations, you need to ensure that you use proper significant figures (which are sometimes called significant digits).
A significant digit (also called a significant figure) is one that is actually measured. The number of significant digits in a measurement depends on the measuring device and the magnitude of its smallest graduation (for example, on most rulers, the smallest graduation is a millimetre). Determining the number of significant figures in a measured quantity requires a few rules. The difficulty occurs primarily when there are zeros. Have a look at the chart to know the rules.
| Rule applied | Examples |
|---|---|
| All digits 1-9 (non-zeros) are significant | 193 has 3 significant figures |
| Zeros between significant digits are significant | 6003 has 4 significant figures |
| Zeros acting as place holders for a decimal point are NOT significant | 0.00345 has only 3 significant figures |
| For numbers greater than 1, trailing zeros are significant only if a decimal point is present | 2.0 has 2 significant figures 20 has only 1 significant figure |
| For numbers less than 1, trailing zeros are always significant | 0.000000980 has 3 significant figures 0.14000 has 5 significant figures |
It is important to be accurate in both the taking and reporting of your measurements. The accuracy of a measurement/numerical value/number can be determined by the number of significant figures it comprises. For this course, many of the measurements presented will have two significant figures, and so many of the answers will have two significant figures as well. There will be exceptions, so please pay attention.
For further understanding of significant figures, read the “Significant Figure Rules (Opens in new window).”
Simple pendulum: Example of periodic motion
For the child on the swing, one complete vibration, or cycle, would require them to swing from the top of one side, down to the bottom, then to the top on the other side, back to the bottom, and then back to where they started. The distance in either direction from the equilibrium, or rest position (when the mass is at rest, hanging vertically), to the maximum displacement (when the mass is at maximum deflection) is called the amplitude.
There are a few words used to describe periodic motion that all mean the same thing.
1 cycle = 1 vibration = 1 oscillation
In the pendulum, when it moves from a to b to c, it has only swung through half a cycle. In order to complete one full cycle, it needs to swing from a over to c then back to a.

Period
Remember

Every time you see this icon, a new formula is being introduced!
The time it takes for an object to go through one complete cycle is called the period. The symbol T is used to represent period, and the units of the period (T) are seconds. To show that the units are in seconds, use an “s”.
Example: 12 seconds is written as 12 s.
Period

where the time is measured in seconds.
Example: Period of a pendulum
The pendulum makes 20 cycles in 5.0 seconds. What is the time needed to complete one cycle?
| Step | Example |
|---|---|
| Given | |
| Unknown | |
| Equation | |
| Solve | |
| Statement |
The time to complete one cycle is 0.25 s |
Note
The period is usually measured in seconds, but larger units of time can be used for convenience if the period is very long. For example, the period of the moon orbiting the Earth is 27.3 days.
Self-Check: Period
Frequency
The number of cycles per second is called frequency (f). The unit of frequency is the hertz (Hz). Note: 1 Hz = 1/s.
Frequency can be calculated using the following equation:

Example: Frequency of a pendulum
A pendulum swings through 12 cycles in 24 seconds. What is the frequency of the pendulum?
| Step | Example |
|---|---|
| Given | |
| Unknown | |
| Equation | |
| Solve | |
| Statement |
The frequency of the pendulum is 0.50 Hz (The pendulum completes 0.5 of a cycle in 1 s) |
Relationship between period and frequency
Go back and look at the period formula. Compare it to the frequency formula. Pause and think – what do you notice?
They are inverses of each other! The formulas are just flipped upside down.
Therefore, if you know the frequency, you can find the period, and if you know the period you can find the frequency quite easily.
Relationship between period and frequency

Example: Period and frequency in a pendulum
A pendulum vibrates 22 times in 11 s. Find the period and the frequency.
| Step | Example |
|---|---|
| Given | |
| Unknown | |
| Equation | |
| Solve |
|
| Statement |
The period of the pendulum is 0.50 s and the frequency of the pendulum is 2 Hz. That means it takes 0.50 s for the pendulum to complete one cycle, and it will complete 2 cycles in one second. |
Amplitude
Amplitude is the distance a particle moves from its rest position.

When the pendulum moves from the rest position to the top of its swing, this is considered the amplitude. In one full cycle, the pendulum will travel four amplitudes.
Example: A swing
A child is sitting on a swing, going back and forth with a constant amplitude of 1.4 m. Find the total horizontal distance that the child moves through in five cycles.

A girl on a swing
Solution
In one cycle, the child moves through four amplitudes. There is a total of five cycles; therefore, the total number of amplitudes = 4 × 5 = 20 amplitudes. Each amplitude is 1.4 m, so the total horizontal distance = 20 x 1.4 m.
The child moves a total horizontal distance of 28 m.
Self-Check: Frequency
Universal wave equation
In this section, you will consider the motion of a wave through a rope and derive an equation for the speed of a wave. Imagine that the rope is tied to a secure position at one end, while you hold the other end in your hand. To make a crest, you would first move your hand rapidly up and then back down to the rest position, followed by moving your hand down and then back up to the rest position to make a trough. As you make this periodic motion, the wave will move through the rope (medium), as shown in the following figure. Remember that each time the source makes one cycle, the wave advances one wavelength.
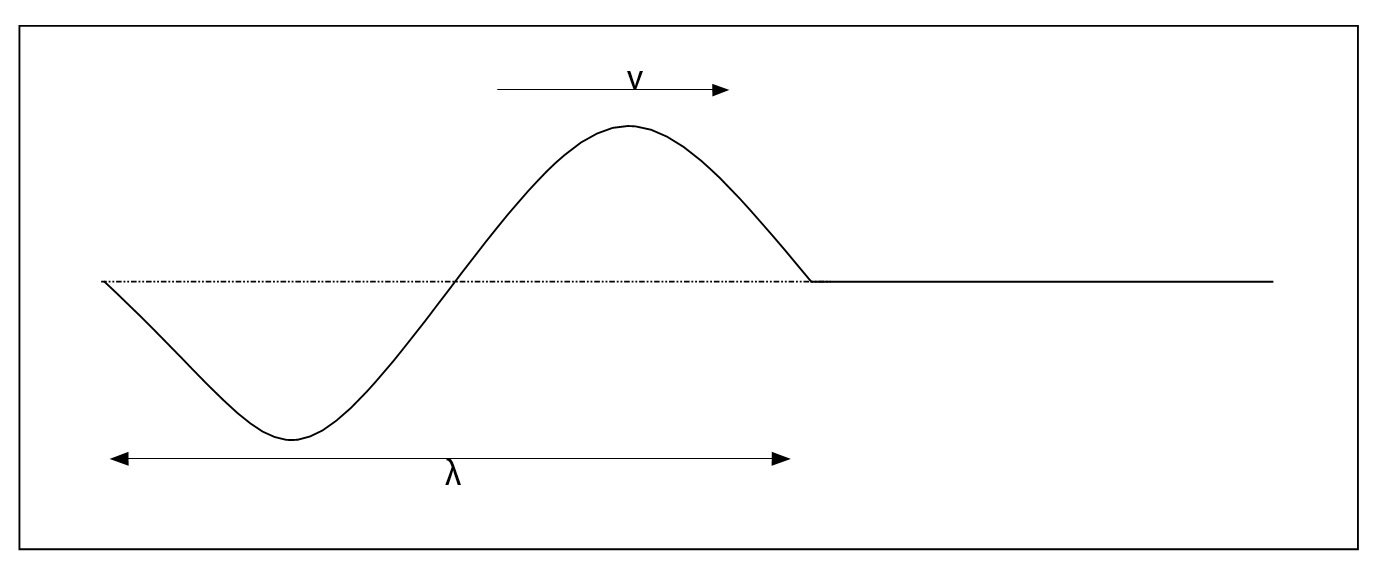
Try it on your own using the “wave on a string” simulation.
Press Enter here for an accessible version of “Wave on a string.” (Opens in new window)
All types of waves keep a constant speed as they move through a medium. For example, if you drop a stone in a bowl of water, the waves created by the stone will travel at the same speed until they reach the edge of the bowl. Since there is no change in speed, the constant speed equation can be used.

Speed of a wave
To analyze the speed of the wave, we must first understand how to calculate the speed:
Speed of a wave

- v represents the speed of the wave, in metres per second (m/s)
- d represents the distance the wave travels, in metres (m)
- t represents the time it takes for the wave to travel, in seconds (s)
The length of the wave has a special name, the wavelength (λ). So instead of using d, use λ. The time for a wave to complete one cycle also has a special name, the period (T). So instead of using t, use T.
This gives us a new formula:
Speed of a wave (continued)

- v represents the speed of the wave, in metres per second (m/s)
- λ represents the length of one cycle of the wave, in metres (m)
- T represents the time for one cycle of the wave to pass by, in seconds (s)
Since there is an inverse relationship between frequency and period, replace /T with f and come up with the universal wave equation:
Universal wave equation

- v represents the speed of the wave, in metres per second (m/s)
- λ represents the length of one cycle of the wave, in metres (m)
- f represents the frequency of the wave, in Hertz (Hz)
This is a very important equation. It is the universal wave equation, which means it works for all types of waves. You can use it to find out about the speed, wavelength, and frequency of water waves, sound waves, light waves, waves in a rope, etc.
Example 1: Universal wave equation
A sound wave has a frequency of 256 Hz and is travelling at 335 m/s. What is the wavelength of the sound wave?
| Step | Example |
|---|---|
| Given | |
| Unknown | |
| Equation | |
| Solve | |
| Statement | The wavelength of the sound wave is 1.31 m. |
Example 2: Water wave
The wavelength of a water wave in a swimming pool is 4.0 m. The wave travels 6.0 m in 2.7 s. Find the frequency of the wave.
| Step | Example |
|---|---|
| Given | |
| Unknown | |
| Equation | |
| Solve |
Tip: v is not given, so use v=d/t first |
| Statement |
The frequency of the water waves is 0.56 Hz. |
Investigate: Speed of a wave
Activity
Now, complete the “wave on a string” simulation to reinforce many of the concepts you have learned about waves, as well as to find out some new ones.
Instructions
- Set the wave to “Pulse.”
- Set the damping to “None.”
- Set it to “Slow motion.”
- Keep it at high tension.
- Click on “Timer” to time the duration of the wave pulse travelling down the string.
- Keep the “Amplitude” and the “Pulse Width” as they are.
Press the green button and watch the waves generate. When it reaches the green bead on one end, start the timer and stop the timer when the wave reaches the other end.
Practise this process until you are comfortable using the timer.
Once you are confident, record your time, reset the timer and repeat the process three more times. Take the average of your four times to get a good approximation of the actual time.
Now, change the amplitude and pulse width. Do the experiment again.Try it a third and fourth time with different combinations of amplitude and pulse width. What did you notice about the time?
If the distance the wave pulse travels in each trial was the same, then what can you conclude about the speed of a wave in the same medium?
The speed of the wave pulse (no matter the amplitude or width) remains constant as long as it is in the same medium.
Self-Check: Universal wave equation
Reflection of waves
When a wave travelling through one medium runs into another medium, it can reflect off the new medium and head back the way it came. This can occur when a sound wave in the air hits a wall, when an ocean wave hits a cliff, and when a transverse wave in a slinky hits the end of the slinky. Examples of this, such as echoes and the properties of sound that make musical instruments work, will be studied in this course.
In the next activity, you will investigate how a wave reflects in two different situations. The first situation will be when the wave hits a fixed end, meaning the end of the wave cannot move. The second situation will be when the wave hits a free (loose) end, meaning the end of the wave can move.
Investigate: Reflection of waves
Press Enter here for an accessible version of “Wave on a string.” (Opens in new window)
Activity
Open the simulation and, in the top left corner, choose “Pulse.” In the top right corner, choose “Fixed End.” Set “Damping” to None. Hit the green button and observe what happens each time the wave gets to the fixed end. You can set it to “Slow motion” if you prefer. Once you feel like you have a good idea of what happens, change the setting to “Loose End” (free end) in the top right and hit the green button. Observe what happens each time the wave gets to the free end. When you feel like you have a good idea of the wave behaviour, watch the videos and then answer the questions.
Fixed end
What happens to the wave when it reaches a fixed end?
The wave flips upside down (inverts). Everything else (amplitude, speed, wavelength) remains the same.
Free end
What happens to the wave when it reaches a free end?
The wave does not flip upside down (does not invert). Everything (amplitude, speed, wavelength) remains the same.
If you did not answer the questions correctly, go back and watch the simulation again to make sure you understand what happens to a wave when it hits a fixed or free end. Remember that the word “invert” means to flip upside down.
Reflecting on your learning
| You are learning about waves and its behaviours. To summarize your learning, reflect on how well you attained the success criteria of this learning activity: | Check one: | ||
| Yes | Beginning to | Not yet | |
| I can distinguish between longitudinal and transverse waves in different media, and provide examples of both types. | |||
| I can calculate both the period and frequency for periodic motion. | |||
| I can explain the relationship between the speed of sound in various media. | |||
| I can solve problems involving wavelength, frequency, and wave speed. | |||
| I can describe the reflection of waves for both fixed and free ends. | |||
Ongoing task: Course formula sheet
An ongoing task that you will be completing in each learning activity is identifying the physics formulas used and recording them in your physical Notebook.
Make sure to have your physical Notebook and a writing utensil (pen or pencil) available at all times.
On the final page of your Notebook, working backwards, write the following heading:
Grade 11 physics formulas
Make sure to leave at least five (5) pages for all the formulas for the course.
Add below it the underlined heading:
Unit 1: Waves and sound
Write down the formulas presented in this learning activity. Then, beside the formulas, write a short note stating in which situation you would use that equation.
Example
Use to find speed of wave: Variable: speed, wavelength, and frequency.
Remember

Throughout the course when you see this icon, be sure to add the new formula to your formula sheet.