Ce qui fait que les mathématiques sont utiles
As-tu déjà été le passager ou le conducteur d’un véhicule qui roulait à 100 kilomètres par heure (km/h)? Probablement. Mais as-tu déjà enfoncé les freins à cette vitesse et dérapé avant de t’arrêter? Prends quelques instants pour imaginer une telle situation, puis regarde l’animation ci-dessous.
Tu ne l’as peut-être pas remarqué sur le coup, mais il existe un lien mathématique entre la vitesse à laquelle tu roulais et la longueur des traces de dérapage.
Si tu utilisais un véhicule pour mesurer la longueur des traces de dérapage à partir de différentes vitesses (p. ex. 100 km/h, 90 km/h, 80 km/h, 70 km/h et ainsi de suite), tu découvrirais qu’il existe une relation quadratique entre la vitesse et la longueur des marques laissées sur la chaussée.
À quoi pourrait servir la définition mathématique de cette relation dans le monde réel? Une personne qui analyse une scène de crime peut mesurer la longueur de tes traces de dérapage et déterminer si tu roulais à une vitesse sécuritaire ou non. La résolution de ce problème il y a de nombreuses années a aidé les forces de l’ordre à recréer des scènes de crime pour d’innombrables accidents de la route, et à désigner ou non une personne fautive.
Tu reverras ce scénario de dérapage à la fin de l'activité d'apprentissage. Arrêtons-nous quelques instants pour connaître un homme qui a enseigné les mathématiques à des étudiants du secondaire qui n’aimaient pas les mathématiques du secondaire.
L’importance de réfléchir à un problème et de tenter de le résoudre toi-même
Dan Meyer est une influente référence dans le domaine de l’enseignement des mathématiques.
Voici quelques renseignements à son sujet :
Bonjour. Je m’appelle Dan Meyer. J’ai enseigné les mathématiques du secondaire à des élèves qui n’aimaient pas les mathématiques du secondaire. Je me suis prononcé en faveur d’un meilleur enseignement des mathématiques ici et sur CNN, Good Morning America, Every Day With Rachel Ray et TED.com. L’université Stanford m’a décerné un doctorat en enseignement des mathématiques et j’occupe actuellement le poste de directeur de l’enseignement à Desmos, où je suis chargé d'explorer l’avenir des mathématiques, de la technologie et de l’apprentissage. J’ai travaillé avec des enseignants dans divers pays et dans l’ensemble des cinquante États des États-Unis. On a dit que je faisais partie des 30 chefs de file de l'avenir dans le domaine de la technologie et de l’apprentissage. Je vis à Oakland, en Californie.
Source : blog.mrmeyer.com/about-2

M. Meyer travaille pour Desmos (s’ouvrira dans une nouvelle fenêtre), une plateforme en ligne dont la capacité de production de graphiques pourrait t’être utile durant le cours.
Comment crois-tu que le fait d’évaluer un problème avant qu’on te donne les étapes à franchir pour le résoudre va :
- Améliorer ton apprentissage?
- Améliorer ta rétention?
- Accroître ton intérêt?
On a conçu ce cours non seulement pour t’enseigner les bases dont tu auras besoin, mais aussi pour te faire réfléchir à la raison pour laquelle tu as commencé ce processus, et ce qui est plus important encore, pour que les mathématiques t’intéressent.
On va entre autres tenter de rendre le contenu intéressant et l’appliquant à ta vie de tous les jours.
Peux-tu penser à des façons dont tu utilises les mathématiques dans la vie de tous les jours?
Les finances, les mesures, la construction, déterminer à quelle heure tu vas arriver à un endroit, le calcul des pourboires, les trajectoires dans les sports, etc.
Ton Journal des mathématiques
Durant le cours, tu créeras un Journal des mathématiques qui couvrira les quatre unités : Introduction aux fonctions quadratiques; Analyse des fonctions quadratiques; Fonctions exponentielles et trigonométrie; Fonctions sinusoïdales. Chacune des unités comprend plusieurs activités d’apprentissage.
À la fin de chacune des activités d’apprentissage, on te demandera de créer une rubrique de journal et on te suggérera le contenu qui devrait s’y trouver. Ces rubriques de journal serviront de résumé pour un grand nombre des concepts les plus importants du cours. Elles te seront utiles quand tu te prépareras aux évaluations de chacune des unités, puis à l’examen final. Voilà pourquoi tu devrais les rédiger de façon à ce qu’elles te soient les plus utiles possible.
N’hésite pas à ajouter au contenu suggéré tout renseignement que tu juges important.
Journal

À la fin du cours, tu devras peaufiner huit rubriques (deux par unité) et les soumettre sous forme de ton « Évaluation de clôture : Journal des mathématiques » (s’ouvrira dans une nouvelle fenêtre). Cette évaluation représente 15 % de ta note.
Quand tu dois ajouter quelque chose à ton Journal des mathématiques, tu verras l’icône suivante.
À l’approche de la fin de chacune des unités, tu auras l’occasion de soumettre une rubrique de ton journal en vue d’obtenir de la rétroaction. Tu pourras ensuite décider d’apporter ou non les corrections recommandées dans la rétroaction, et d’ajouter ou non la rubrique en question à ton évaluation de clôture. Si tu conserves les quatre rubriques en question, tu auras déjà la moitié des rubriques requises avant même d’avoir atteint la fin du cours!
Chacune des huit rubriques de journal que tu soumettras doit comprendre ce qui suit :
- la rubrique de journal pour l’activité d’apprentissage en question;
- des « preuves » de l’apprentissage tiré de l’activité (photos d’exemples traités, explications écrites, feuille sommaire, etc.).
Les rubriques de ton Journal des mathématiques peuvent prendre bien des formes.
Voici quelques suggestions :
- Journal manuscrit (numérisé)
- Journal en ligne
- Vidéos
- Images ou photos
- Enregistrements audio
Évaluation de clôture MCF3M Grille d’évaluation du Journal des mathématiques
Prends connaissance de la grille d’évaluation ci-dessous pour t’assurer de bien comprendre les lignes directrices d’évaluation.
|
Critères de réussite |
Niveaux |
|---|---|
|
(À noter : les critères de réussite ne s’appliquent pas nécessairement à toutes les rubriques de ton journal) La rubrique de journal sélectionnée démontre : |
La rubrique de journal sélectionnée démontre les critères de réussite suivants : |
|
Niveau 4 (80 % à 100 %)
Niveau 3 (70 % à 79 %)
Niveau 2 (60 % à 69 %)
Niveau 1 (50 % à 59 %)
|
|
Critères de réussite |
Niveaux |
|---|---|
|
(À noter : les critères de réussite ne s’appliquent pas nécessairement à toutes les rubriques de ton journal) La rubrique de journal sélectionnée démontre : |
La rubrique de journal sélectionnée démontre les critères de réussite suivants : |
|
Niveau 4 (80 % à 100 %)
Niveau 3 (70 % à 79 %)
Niveau 2 (60 % à 69 %)
Niveau 1 (50 % à 59 %)
|
|
Critères de réussite |
Niveaux |
|---|---|
|
(À noter : les critères de réussite ne s’appliquent pas nécessairement à toutes les rubriques de ton journal) La rubrique de journal sélectionnée démontre : |
La rubrique de journal sélectionnée démontre les critères de réussite suivants : |
|
Niveau 4 (80 % à 100 %)
Niveau 3 (70 % à 79 %)
Niveau 2 (60 % à 69 %)
Niveau 1 (50 % à 59 %)
|
|
Critères de réussite |
Niveaux |
|---|---|
|
(À noter : les critères de réussite ne s’appliquent pas nécessairement à toutes les rubriques de ton journal) La rubrique de journal sélectionnée démontre : |
La rubrique de journal sélectionnée démontre les critères de réussite suivants : |
|
Niveau 4 (80 % à 100 %)
Niveau 3 (70 % à 79 %)
Niveau 2 (60 % à 69 %)
Niveau 1 (50 % à 59 %)
|
Déterminer le type de relation à partir
de graphiques, de tableaux et d’équations
Sujet 1
Il existe trois façons de déterminer si une relation est linéaire, quadratique ou ni l’une ni l’autre :
- à partir d’un graphique;
- à partir d’une table de valeurs;
- à partir d’une équation.
Déterminer le type de relation à partir d’un graphique
Certaines représentations sont représentées par une ligne sur un graphique. C’est ce qu’on appelle les relations linéaires. Certaines représentations sont représentées par une parabole sur un graphique. Les paraboles ont une forme unique que tu peux voir ci-dessous. C’est ce qu’on appelle des relations quadratiques.
Peux-tu donner deux exemples où tu vois des équations linéaires dans ta vie?
Routes, vitesse, quantité d’essence qui reste dans le réservoir alors que tu conduis ta voiture, etc.
Peux-tu donner deux exemples où tu vois des équations quadratiques dans ta vie?
Lancer une balle, frapper une balle de golf, balançoires, plongeon, etc.
Le sommet
Les paraboles sont associées à de nombreuses caractéristiques, dont l’orientation de l’ouverture concave (vers le haut ou vers le bas) et un point que l’on appelle le sommet. Le sommet d’une parabole a des coordonnées (x, y) distinctes et représente soit la valeur maximale soit la valeur minimale de y. Prends un instant pour explorer les relations entre d’un côté le sommet et de l’autre la forme et l’orientation de la parabole et sélectionnant le sommet et en le déplaçant à diverses positions.
Déterminer le type de relation à partir d’une table de valeurs
Tim Jurinder est propriétaire de TJ’s Garage. Pour réparer une voiture, TJ’s Garage exige des frais initiaux de 20 $, plus 40 $/h.
Créons une table de valeurs représentant cette situation (le montant facturé dépend du nombre d’heures travaillées).
Utilise 0, 1, 2, 3, 4 pour les heures travaillées, puis trouve les Montants facturés selon le nombre d’heures travaillées à TJ’s Garage :
|
Heures |
Montant facturé |
|---|---|
|
0 |
20 + 40(0) = 20 |
|
1 |
20 + 40(1) = 60 |
|
2 |
20 + 40(2) = 100 |
|
3 |
20 + 40(3) = 140 |
|
4 |
20 + 40(4) = 180 |
Voici un graphique des valeurs en question et des Montants facturés selon le nombre d’heures travaillées à TJ’s Garage :
Comme tu peux le voir, la table de valeurs indique une relation linéaire.
Déterminer le type de relation à partir des différences premières
Pour confirmer cela de manière algébrique, on peut trouver les différences premières. Les différences premières nous indiquent à quel point la relation change à la verticale pour tout changement horizontal.
Si les différences premières sont constantes, on peut en arriver à la conclusion que la relation en est une de diminution ou d’augmentation constante, ce qui veut dire que la relation est linéaire.
On va maintenant trouver les différences premières et déterminer si elles sont constantes ou non en soustrayant les valeurs de y dans le tableau. On soustrait les valeurs de bas en haut. N’oublie pas que pour qu’il soit possible d’utiliser les différences pour établir le type de relation, il faut que la hausse ou la baisse des valeurs de x soit constante.
| Heures | Montant facturé |
|---|---|
| 0 | 20 |
| 1 | 60 |
| 2 | 100 |
| 3 | 140 |
| 4 | 180 |
| Différences premières |
|---|
| }
60 – 20 = 40 |
| }
100 – 60 = 40 |
| }
140 – 100 = 40 |
| }
180 – 140 = 40 |
La relation est-elle linéaire? Explique ta réponse.
Il s'agit d'une relation linéaire, car les différences premières sont constantes.
Déterminer le type de relation dans une table de valeurs à partir des différences secondes
On peut appliquer le même concept pour déterminer si une relation est quadratique. Si une relation est quadratique, les différences secondes sont constantes. On obtient les différences secondes en soustrayant la différence première. Les différences premières des relations linéaires affichent des hausses et des baisses d’une quantité constante. On peut dire la même chose des différences secondes pour les équations quadratiques.
Comparer deux ensembles de données grâce à deux tables de valeurs
Calcule la différence première et seconde pour déterminer si les deux tables représentent une relation linéaire, quadratique ou ni une ni l’autre.
| 0 | 4 |
| 1 | 6 |
| 2 | 8 |
| 3 | 10 |
| 4 | 12 |
| Différences premières |
|---|
| }
(soustraire les valeurs de y de bas en haut) 6 - 4 = 2 |
| }
8 – 6 = 2 |
| }
10 – 8 = 2 |
| }
12 – 10 = 2 |
| Différences secondes |
|---|
| }
2 – 2 = 0 |
| }
2 – 2 = 0 |
| }
2 – 2 = 0 |
Encore une fois, calcule les différences premières et secondes.
| 0 | 4 |
| 1 | 10 |
| 2 | 12 |
| 3 | 10 |
| 4 | 4 |
| Différences premières |
|---|
| }
(soustraire les valeurs de y de bas en haut) 10 - 4 = 6 |
| }
12 – 10 = 2 |
| }
10 – 12 = -2 |
| }
4 – 10 = -6 |
| Différences secondes |
|---|
| }
2 – 6 = -4 |
| }
-2 – 2 = -4 |
| }
(-6) - (-2) = - 6 + 2 = -4 |
Comment déterminer si une relation est linéaire ou quadratique grâce à une table de valeurs
Maintenant, déterminer si les tables ci-dessus représentent des relations linéaires ou quadratiques.
Confirme que les valeurs de x augmentent ou diminuent d’une quantité constante
Est-ce que les valeurs de x augmentent d’une quantité constante dans les deux tables de valeurs?
Oui.
Détermine les différences premières en soustrayant les valeurs de y de bas en haut
Si les différences premières sont les mêmes (constantes), la table représente une relation linéaire
Selon les différences premières, est-ce que la première table est linéaire? Comment le sais-tu?
Oui. Les différences premières de la première table sont constantes.
Selon les différences premières, est-ce que la deuxième table est linéaire? Comment le sais-tu?
Non. Les différences premières de la deuxième table ne sont pas constantes.
Si les différences premières ne sont pas constantes, déterminer les différences secondes en soustrayant les différences premières. Si les différences secondes sont constantes, la table représente une relation quadratique.
Selon les différences secondes, est-ce que la deuxième table est quadratique? Comment le sais-tu?
Oui, la deuxième table est quadratique. Les différences secondes sont constantes.
Déterminer le type de relation à partir d’une équation
Forme d’une équation linéaire
Une fonction linéaire peut se présenter dans la forme suivante :
Elle représente une relation linéaire, car il s’agit d’un polynôme de degré 1. L’exposant le plus élevé appliqué à la variable est 1
Exemples d’équations linéaires
On recherche toujours le degré après avoir développé et simplifié l’équation.
Forme d’une équation quadratique
Une fonction quadratique peut se présenter dans la forme suivante :
Elle représente une relation quadratique, car il s’agit d’un polynôme de degré 2. L’exposant le plus élevé appliqué à la variable est 2
Exemples d’équations quadratiques
Déterminer le degré d’une relation
sans utiliser un graphique ou une table de valeurs
Sujet 2
Pour déterminer le degré d’une relation sans faire appel à un graphique ou à une table de valeurs, du dois faire ce qui suit :
- Tout d’abord, fais toutes les multiplications nécessaires (développement).
- Ensuite, fais toutes les additions et les soustractions (simplification).
- Troisièmement, regarde le résultat et détermine le degré de la relation.
Développe l’équation
Pour développer, on multiplie les termes.
Tu dois de rappeler d’appliquer la distributivité en développant l’équation en supprimant les parenthèses. Multiplie tous les termes ensemble.
Simplifie l'équation.
Pour simplifier, on additionne ou soustrait des termes.
On ne simplifie que les termes semblables, c'est-à-dire les termes qui ont les mêmes exposants sur les mêmes variables.
On additionne ou soustrait les coefficients des termes semblables.
Exerce-toi à déterminer le degré d’une relation en traitant un exemple tiré de la vraie vie.
Tu déménages dans une nouvelle maison qui a une chambre à coucher de forme carrée dont l’aire représente le triple de celle de ta chambre actuelle (qui est elle aussi carrée). Détermine une expression simplifiée pour ta nouvelle chambre si la relation suivante décrit la longueur des côtés de ta chambre actuelle .
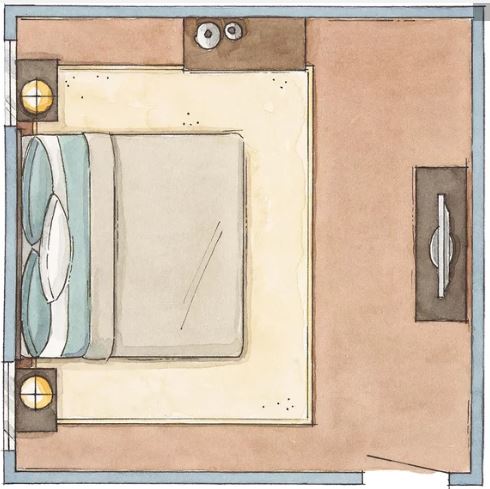
Si l’équation n’a pas été donnée, il faut la construire
N’oublie pas qu’on recherche l’équation qui décrit une chambre dont l’aire représente le triple de la chambre qu’on te montre.
La formule pour déterminer l'aire d'un carré est ).
Développe les binômes en faisant appel à la distributivité
N’oublie pas d’écrite le binôme deux fois, car il est au carré
Rappelle-toi que la distributivité veut dire qu’il faut multiplier chacun des termes dans une parenthèse par tout ce qui se trouve dans l’autre parenthèse.

Développe le monôme grâce à la distributivité
Rappelle-toi de multiplier le nombre devant la parenthèse par tous les termes à l’intérieur de la parenthèse

Simplifie les termes semblables
Rappelle-toi qu’on additionne ou soustrait les coefficients des termes semblables
Voici donc une expression simplifiée de l’air de la nouvelle chambre :
Passe en revue ce que tu sais de la détermination d’un type de relation
Dans la mise en situation, tu as lu que M. Dan Meyer travaille pour Desmos (s’ouvrira dans une nouvelle fenêtre). Prends un instant pour explorer le site de Desmos en créant un graphique linéaire et une parabole. Prends des captures d’écran de tes graphiques pour pouvoir y retourner.
Autovérification
En tant qu’apprenante ou apprenant autonome, tu devras réfléchir à ton processus d’apprentissage et vérifier ta compréhension afin de pouvoir planifier ta réussite. Note ta compréhension des critères de réussite liés à l’activité d’aujourd’hui.
Journal

Crée un tableau comme celui-ci dans ton Journal des mathématiques (s’ouvrira dans une nouvelle fenêtre). Remplis-le dans Desmos ou tout autre outil de création graphique auquel tu as accès.
|
Exemple de graphique de relation linéaire de Desmos |
Exemple de graphique de relation quadratique de Desmos |
|---|---|
Passe en revue les critères de réussite
Évalue ta compréhension selon une échelle de 5 à 1.
5 signifie que « je comprends pleinement le concept ». 1 signifie que « je suis confuse ou confus ».
Journal

Prends maintenant quelques instants pour résumer, dans tes propres mots, comment déterminer si une relation est linéaire, quadratique ou ni une ni l’autre selon un graphique, une table de valeurs ou une équation.
Voici une suggestion de façon d’organiser le tableau dans ton Journal des mathématiques.
|
À partir d’un graphique |
À partir d’une table de valeurs |
À partir d’une équation |
|
|---|---|---|---|
|
Linéaire |
|||
|
Quadratique |
Résume, dans tes propres mots, ce que signifie de développer une expression, par rapport à simplifier cette expression
Autres exercices avec les relations quadratiques
Réfléchis à la relation . Remplis la table ci-dessous pour cette relation. Quand tu auras terminé, compare tes réponses aux réponses suggérées.
|
-4 |
-16 |
|
-3 |
-9 |
|
-2 |
-4 |
|
-1 |
-1 |
|
0 |
0 |
|
1 |
-1 |
|
2 |
-4 |
|
3 |
-9 |
|
4 |
-16 |
| Différences premières |
|---|
| }
7 |
| }
5 |
| }
3 |
| }
1 |
| }
-1 |
| }
-3 |
| }
-5 |
| }
-7 |
| Différences secondes |
|---|
| }
-2 |
| }
-2 |
| }
-2 |
| }
-2 |
| }
-2 |
| }
-2 |
| }
-2 |
Selon les données de la table, comment peux-tu savoir qu’il s’agit d’une équation quadratique?
Dans la table, les différences secondes sont constantes, alors la relation est quadratique.
Selon l’équation, comment peux-tu savoir qu’il s’agit d’une équation quadratique?
L’équation est de degré 2, alors la relation est quadratique.
Trace le graphique de la relation.
Dans quelle direction s’ouvre la parabole?
La parabole s’ouvre vers le bas, ce qu’on appelle une concavité vers le bas.
Désigne le sommet. Est-ce qu’il s’agit d’un minimum ou d’un maximum?
Le sommet se trouve à (0,0) et il s’agit d’un maximum.
Quel lien peux-tu établir entre les différences secondes et la direction dans laquelle s’ouvre la parabole?
Quand des différences secondes sont positives, la concavité de la parabole est vers le haut.
Quand des différences secondes sont négatives, la concavité de la parabole est vers le bas.
Quel lien peux-tu établir entre la concavité d’une parabole et le fait qu’elle a un point minimum ou maximum?
Une parabole qui s’ouvre vers le bas comporte un maximum, alors qu’une parabole qui s’ouvre vers le haut a un minimum.
Autre exemple de relations quadratiques dans une situation réaliste
Les équations quadratiques sont en jeu dans de nombreuses situations réelles, comme vous pouvez le voir dans l’exemple ci-dessous qui porte sur les traces de freinage.
Lors d’une enquête sur un accident de voiture, les forces de l’ordre mesurent la longueur des traces de freinage sur la route. L’enquêteur sait que la distance de dérapage d’une voiture dépend de la vitesse à laquelle roule la voiture avant qu’on appuie sur les freins.
Suppose que le conducteur appuie sur les freins et dérape à une intersection de façon a la traverser alors que le feu est au rouge. L’enquêteur utilise la table de valeurs suivante pour déterminer la vitesse de la voiture :

| Vitesse (km/h) | Longueur du dérapage (m) |
|---|---|
| 0 | 0 |
| 10 | 0,7 |
| 20 | 2,8 |
| 30 | 6,3 |
| 40 | 11,2 |
| 50 | 17,5 |
| 60 | 25,2 |
| 70 | 34,3 |
| 80 | 44,8 |
| 90 | 56,7 |
| 100 | 70 |
À l’aide d’un papier et d’un crayon, réponds aux questions suivantes par toi-même. Quand tu auras terminé, compare tes réponses aux réponses suggérées.
Crée la courbe qui correspond le mieux possible à ces données.
Sur une feuille de papier quadrillé, dessine un axe vertical (ordonnées ou y) et un axe horizontal (abscisses ou x).
- L’axe horizontal représente la vitesse (km/h) et l’axe vertical représente la longueur du dérapage (m).
- Sélectionne une échelle qui convient pour l’axe horizontal. Par exemple, un carré pourrait représenter 10 km/h. Pour l’axe vertical, disons qu’un carré représentera 20 m. Conseil : laisse-toi de la place sur ton graphique pour trouver la vitesse d’une voiture qui laisse une trace de freinage de 80 m.
- Trace un graphique à l’aide des couples de la table de valeurs : (0, 0), (10, 0,7), (20, 2,8), (30, 6,3) et ainsi de suite.
- Dessine une courbe lisse pour relier les points.
- Donne au graphique le titre suivant : Longueur du dérapage et vitesse
Les policiers ont observé une trace de dérapage de 80 m de long. Utilise la courbe pour estimer la vitesse de la voiture.
- Prolonge le graphique en suivant la même courbe ou tendance pour les données.
- Situe où se trouve la valeur de 80 m sur l’axe vertical.
- Trace une ligne horizontale dans la version prolongée du graphique.
- Marque ce point.
- Trace une ligne verticale jusqu'à rencontrer l’axe horizontal.
- Estime la vitesse de la voiture.
On arrive donc à la conclusion que la voiture roulait à environ 107 km/h.
Détermine les différences secondes pour confirmer s’il s’agit ou non d’une équation quadratique. Il te sera utile de continuer à remplir la table.
| Vitesse (km/h) | Longueur du dérapage (m) |
|---|---|
| 0 | 0 |
| 10 | 0,7 |
| 20 | 2,8 |
| 30 | 6,3 |
| 40 | 11,2 |
| 50 | 17,5 |
| 60 | 25,2 |
| 70 | 34,3 |
| 80 | 44,8 |
| 90 | 56,7 |
| 100 | 70 |
| Différences premières |
|---|
| }
0,7 |
| }
2,1 |
| }
3,5 |
| }
4,9 |
| }
6,3 |
| }
7,7 |
| }
9,1 |
| }
10,5 |
| }
11,9 |
| }
13,3 |
| Différences secondes |
|---|
| }
1,4 |
| }
1,4 |
| }
1,4 |
| }
1,4 |
| }
1,4 |
| }
1,4 |
| }
1,4 |
| }
1,4 |
| }
1,4 |
Selon ce que tu as trouvé, est-ce qu’il s’agit d’une équation quadratique? Explique pourquoi.
Les différences secondes sont constantes, ce qui confirme que la relation est quadratique.
Pourquoi n’utilises-tu pas de valeurs négatives pour la vitesse ou la longueur des traces dans cette situation?
Les valeurs négatives ne fonctionnent pas dans cette situation, car une vitesse négative et une longueur de marques négative ne s’appliquent pas dans des situations réelles. On mesure la vitesse et la longueur à l’aide de valeurs positives seulement.
Remarque : L’extrapolation est le processus qui consiste à prolonger un graphique pour faire une prédiction au-delà d’un ensemble précis de données.


