Une majeure en physique?
Tu envisages une carrière en physique? Alors que tu te prépares pour l'université, tu te demandes peut-être :
« Que peut-on faire avec une majeure en physique? »
Le salaire de ceux qui terminent une majeure en physique peut varier considérablement. Tout dépend du niveau d'études et de la nature précise de l’emploi occupé.
Effectue l'activité ci-dessous en remplissant les espaces vides afin de compléter la description des emplois illustrés dans les images. Es-tu capable de deviner combien quelqu’un peut gagner dans chacun de ces excellents emplois dans le domaine de la physique?

Maintenant que tu as identifié et que tu peux décrire certains des emplois liés au domaine de la physique, ce cours te permettra d'acquérir les connaissances de base pour démontrer tes compétences en matière d’investigation scientifique (autant pour l'enquête que pour la recherche) dans les quatre domaines de compétences suivants : l’initiative et la planification, l’exécution et la consignation des résultats, l’analyse et l’interprétation, et enfin la communication.
Commençons par l'initiative et la planification pour te préparer à réussir ce cours en ligne.
Révision des vecteurs
Lors du cours préalable à celui-ci, SPH3U, tu as étudié les ondes et leur fréquence, mouvement, accélération, position et vitesse.
Besoin de rafraîchir tes connaissances?
Regarde cette vidéo intitulée "Introduction à la quantité de mouvement" pour te rafraîchir la mémoire quant aux concepts sur lesquels ce cours-ci s'appuiera.
La mécanique est la division de la physique qui étudie le mouvement. Peu importe quel domaine des sciences ou du génie t’intéresse, la mécanique y joue un rôle important - le mouvement est une notion fondamentale dans toutes les sciences. Quand nous poursuivrons notre étude de la physique du mouvement, évite de mémoriser l’information. Concentre-toi plutôt sur son sens et ses applications. Le but est de t’aider à acquérir une certaine aisance avec la terminologie employée dans l’étude de la mécanique.
Les scalaires, les vecteurs, la distance, le déplacement, la vitesse, la vélocité et l’accélération.
On emploie fréquemment ces mots pour décrire le mouvement des objets. Ton objectif devrait être de bien te familiariser avec leur signification.
Qu’est donc un vecteur et que représente-t-il dans la vie quotidienne?
Un vecteur est une quantité qui possède une grandeur ainsi qu’une direction. Ce terme est employé en mathématiques, en génie et surtout en physique; les quantités scalaires, quant à elles, sont des valeurs qui sont uniquement définies par leur grandeur.
Carnet de notes
Vérifions si tu comprends bien la distinction. Dans ton carnet de notes, recrée le tableau ci-dessous et réfléchis aux quantités suivantes. Détermine si chaque quantité est un vecteur ou un scalaire. Appuie ensuite sur le bouton pour voir la réponse. Combien de réponses correctes as-tu obtenues?
Carnet de notes
Parmi les exemples de vecteurs, on trouve diverses quantités comme le déplacement, la force, la vélocité, la quantité de mouvement, l'accélération et bien d'autres encore. Sachant cela, réfléchis aux activités quotidiennes qui impliquent des vecteurs.
Les vecteurs ont un rôle à jouer dans presque toutes nos activités. Un vecteur est une quantité qui a une grandeur et une direction.
Voici quelques exemples d’activités quotidiennes qui impliquent des vecteurs :
- Respirer → Les muscles du diaphragme exercent une force qui a une grandeur et une direction.
- Marcher → On marche à une vélocité d’environ 6 km/h en direction de la salle de bain.
- Aller manger → Le déplacement des élèves de la salle de classe à la cafétéria est d’environ 40 m en direction nord.
Chaque quantité vectorielle a une grandeur et une direction. Il peut t’être utile de noter ceci dans ton carnet de notes.
Quand on étudie la physique, la capacité de représenter de façon visuelle les concepts physiques est très importante. Le monde que cette science étudie est un monde physique - il s’agit du monde que nous pouvons voir.
Par conséquent, la capacité de visualiser et de créer des représentations visuelles des concepts abordés en physique nous aide à les concrétiser et à en avoir une compréhension plus approfondie.
Commence tout de suite à cultiver tes habiletés en visualisation. Penchons-nous maintenant sur l'utilisation de diagrammes pour décrire le mouvement des objets.
Les diagrammes vectoriels décrivent la direction et la grandeur relative d'une quantité vectorielle au moyen d’une flèche de vecteur. Les diagrammes vectoriels peuvent servir à décrire la vélocité d'un objet pendant son mouvement.
On pourrait donc par exemple représenter le mouvement d'une voiture qui se déplace sur la route à l’aide d’un diagramme vectoriel.

Essaie!
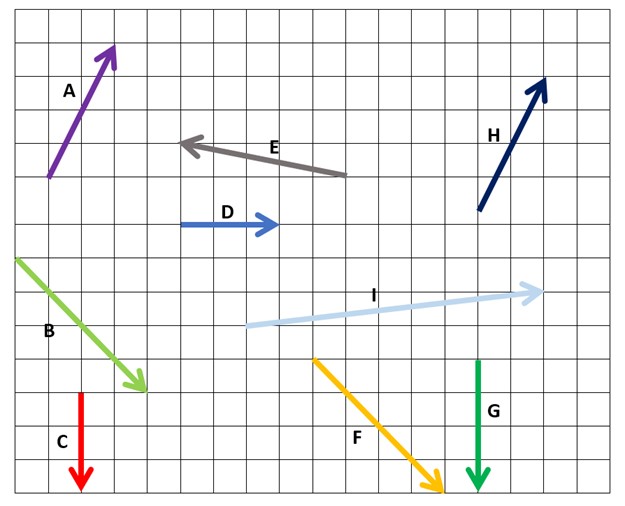
Révisons ce que nous avons appris au sujet des vecteurs. Examine les vecteurs A à I dans la grille ci-dessous. Classe les vecteurs du tableau en utilisant la lettre correspondante (A, B, etc.)
Quantités scalaires et quantités vectorielles
Les mesures du mouvement entrent dans l'une des deux catégories suivantes : Les mesures scalaires et les mesures vectorielles.
Pour décrire le mouvement, on utilise des quantités scalaires et des quantités vectorielles, car la grandeur (la valeur numérique) et la direction sont toutes deux importantes.
Quantités scalaires : quantités composées d’un nombre (la grandeur) et des unités appropriées.
Les mesures scalaires, comme le temps, la masse, la vitesse et la distance, ont des valeurs numériques et une unité de mesure. Par exemple :
- Temps = s
- Vitesse = v = 80 m/s
- Distance =
- Masse = m = 10 kg
Quantités vectorielles : quantités composées d’un nombre (la grandeur), des unités appropriées et d’une direction.
Les quantités vectorielles, comme le déplacement, la vélocité et l’accélération, comprennent des valeurs numériques, une unité de mesure et une direction. Par exemple :
- Déplacement [est]
- Vélocité = [sud]
- Accélération [vers le bas]
Remarque que les variables qui représentant des vecteurs ont des flèches au-dessus. Chaque fois qu’on précise une quantité vectorielle au moyen d’une valeur et d’une direction, on ajoute le symbole vectoriel (la flèche) au-dessus de la variable.
Les vecteurs à deux dimensions
Carnet de notes
Examine les vélocités suivantes :
[vers l’avant]
Notons que, pour les besoins de ce cours, « vers l’avant » ou « avancer » signifie que le vecteur est horizontal et pointe vers la droite. Autrement dit, ce vecteur-ci est dirigé vers l’est.
[sud] (On pourrait aussi écrire « 65 km/h [S] ».)
[ouest 25° nord]
[sud 10° est]
Dans ton carnet de notes, copie les vélocités ci-dessus et réponds aux questions suivantes :
1. Qu’est-ce que ces vélocités ont en commun?
2. Quelles différences y a-t-il dans la façon dont elles sont représentées?
Toutes ces vélocités ont une grandeur, des unités et une direction; cela dit, ces caractéristiques sont différentes pour chaque valeur.
Par exemple, si nous regardons de près les deux premiers vecteurs, et , nous constatons qu'une seule composante directionnelle est nécessaire pour les décrire; ce sont des vecteurs unidimensionnels.


Pour ce qui est des deux derniers vecteurs, et , il faut deux composantes directionnelles et un angle pour les définir clairement; il s’agit donc de (vecteurs bidimensionnels). On peut représenter ces vélocités (ou « vitesses vectorielles ») par des vecteurs dessinés à l'échelle, comme tu peux le voir ci-dessous.


La description des vecteurs
Un vecteur est représenté par une flèche, avec une « tête » (aussi appelé sa « pointe ») et une « queue », comme illustré ci-dessous. La pointe de la flèche indique la direction du vecteur.

La représentation graphique et numérique des vecteurs
Considérons par exemple ce vecteur de déplacement représenté graphiquement à côté d'un point de référence. Dans le présent cours, une rose des vents à quatre pointes indiquant le nord, le sud, l’est et l'ouest constitue souvent le point de référence employé.

Ce vecteur de déplacement peut être représenté graphiquement ou numériquement, comme suit :
8 m [E] ou 8 m [est].
Tous les vecteurs ont une direction, mais ils ne pointent pas tous directement vers le nord, le sud, l'est ou l'ouest. Par conséquent...
Comment exprimerais-tu la direction d’un vecteur?
Il existe plusieurs façons convenables d’exprimer la direction d'un vecteur en deux dimensions.
Dans le diagramme ci-dessous, un vecteur pointe à 50° à l'est du nord. Autrement dit, on pourrait indiquer la direction du vecteur en commençant au nord puis en le déplaçant de 50° vers l'est.
Au lieu de dessiner le vecteur, tu peux également l'exprimer au moyen de la notation écrite.
Pour cet exemple, on écrirait donc [N 50° E]. Les crochets indiquent qu'il s'agit d'une notation vectorielle. L'exemple ci-dessus utilise le nord, l'est, le sud et l'ouest pour préciser la direction du vecteur, mais on peut également la décrire d’autres façons.

Voyons quelques exemples.
Exemple 1
Une vélocité de 80 km/h [NO] ou [N 45° O]
![Vélocité de 80 km/h [NO]](../assets/img/sph4u_01.01.11.svg)
Exemple 2
Une accélération de 5 m/s² [S 25° E] ou [E 65° S]
![Accélération de 5 mètres par seconde au carré [S 25° E]](../assets/img/sph4u_01.01.12.svg)
Autovérification et réflexion
Il s’agit d’une autovérification qui peut t’aider à :
- évaluer ton propre travail;
- déterminer la progression de ton apprentissage, ce qu’il te reste à apprendre et la meilleure façon d’atteindre tes objectifs;
On te donnera des suggestions de réponses que tu pourras comparer à tes propres réponses.
Après avoir vérifié tes réponses, pose-toi les questions de réflexion suivantes :
- Quels sont les concepts qu’il me reste à approfondir?
- Qu’est-ce que j’ai bien fait?
- Que dois-je faire maintenant pour m’assurer que j’ai compris tous les concepts?
- Quelles mesures puis-je prendre pour m’améliorer et grandir en tant qu’apprenant?
Donne la direction de chacun des trois vecteurs ci-dessous.
Vecteur 1 :
[SO] ou [S 45° O]

Vecteur 2 :
[E 25° N] ou [N 65° E]
![Accélération de 5 mètres par seconde au carré [S 25° E]](../assets/img/sph4u_01.01.14.svg)
Vecteur 3 :
[N 15° O] ou [O 75° N]

Exercice : La représentation des vecteurs
Dans un diagramme vectoriel, la grandeur d'une quantité vectorielle est représentée par la taille de la flèche du vecteur. Si la taille de la flèche dans chaque section consécutive du diagramme vectoriel est la même, alors la grandeur de ce vecteur est constante.
Question 1 :
Examine chacun des diagrammes vectoriels à gauche et donnes-en la direction à droite.
Pour la prochaine série de questions à choix multiples, étudie chaque diagramme vectoriel et choisis la bonne direction.
Le dessin des vecteurs
Dans certaines situations, il est utile de faire un dessin à l'échelle des vecteurs. Dans de tels cas, on doit toujours inclure une déclaration du genre
« Sois 1 cm = 2 m » pour indiquer l’échelle du dessin. Selon cet exemple, pour représenter un vecteur de 10 m de long, on peut en dessiner un de 5 cm de long et ajouter la mention « 1 cm = 2 m ».
Carnet de notes
Pour effectuer les tâches de cette section, il te faudra une règle, un rapporteur d'angles et un compas.
Examinons les vecteurs de vélocité qui ont été mentionnés précédemment :
- = 2,4 m/s [vers l’avant].
- = 65 km/h [sud] (On pourrait aussi écrire « 65 km/h [S] ».)
- = 14 cm/s [ouest 25° nord]
- = 7,5 m/min [sud 10° est]

Notons que, pour les besoins de ce cours, « vers l’avant » ou « avancer » signifie que le vecteur est horizontal et pointe vers la droite. Cela veut dire que le vecteur est dirigé vers l’est.
On peut représenter ces vélocités par des vecteurs dessinés à l'échelle, comme tu peux le voir ci-dessous.
Choisis une échelle facile à représenter dans un dessin. Pour déterminer la longueur de la ligne que tu dois tracer, prends-en la grandeur originale et divise-la par l'échelle choisie.


Voici les dessins à l’échelle pour et ci-dessus.


Pour dessiner des vecteurs qui ne sont pas orientés directement vers l’un des points cardinaux (N, S, E, O), il est nécessaire de travailler à partir d'un point de référence qui a ses propres directions de compas.
Carnet de notes
Dans ton carnet de notes, suis les indications ci-dessous pour dessiner des vecteurs dont la direction est en angle.
Exercice : La représentation des directions de vecteurs
Carnet de notes
Pour les questions suivantes, dessine chaque vecteur à l’aide de ta règle et de ton rapporteur d'angles.
N’oublie pas d’indiquer sur chaque diagramme l’échelle que tu as employée.
L’addition des vecteurs
Nous avons appris que les vecteurs comprennent deux éléments : leur grandeur et leur direction. La déconstruction d'un vecteur en ses composantes horizontale et verticale constitue une technique fort utile pour comprendre les problèmes de physique.
Réfléchis aux activités suivantes et au rôle qu’y jouent les vecteurs :
Traverser une rivière en bateau à la rame.
Piloter un avion quand il y a du vent.
Chaque fois que tu vois un mouvement avec un angle, tu dois le considérer comme un déplacement à la fois horizontal et vertical. Le fait de simplifier les vecteurs de cette façon accélère les calculs et permet de suivre le mouvement des objets.
Les composantes des vecteurs
La composante horizontale s'étend du début du vecteur jusqu’à sa coordonnée x la plus éloignée. La composante verticale s'étend de l'axe des x jusqu'au point vertical le plus élevé du vecteur. Ces deux composantes et le vecteur forment ensemble un triangle rectangle.

À visionner
Regarde cette vidéo de M. Andersen qui récapitule les différences entre les quantités scalaires et les quantités vectorielles. Il y donne également une démonstration de l'importance des vecteurs et de l’addition vectorielle à partir de 4 min 46 secondes.
Introduction aux vecteurs et aux scalaire(s’ouvrira dans une nouvelle fenêtre)
Le lien vers cette vidéo est uniquement fourni à titre de suggestion. On t'encourage à trouver d'autres ressources pour parfaire ta compréhension.
- Coordonnées : Nombres indiquant une position par rapport à un axe donné. Exemple : Les coordonnées x et y indiquent la position d’un point par rapport aux axes des x et des y.
- Axe : Droite imaginaire autour de laquelle un objet effectue sa rotation ou est disposé symétriquement.
- Grandeur : Nombre attribué à un vecteur et indiquant sa longueur.
Si l’on prend le vecteur à analyser comme hypoténuse, on peut en déterminer les composantes horizontale et verticale en complétant un triangle rectangle. Le bord inférieur du triangle constitue la composante horizontale du vecteur, et le côté opposé à l'angle en est la composante verticale.
Avant de nous plonger réellement dans l'addition de vecteurs, rafraîchissons nos souvenirs des mathématiques...
Hypoténuse
sinus
d’un triangle rectangle
cosinus
a² + b² = c²
tangente
Révision des triangles pythagoriciens et de la trigonométrie
Regarde les vidéos suivantes pour réviser les concepts mathématiques du théorème de Pythagore et de la trigonométrie à angle droit avant de continuer cette section.
- La relation de Pythagore (s’ouvrira dans une nouvelle fenêtre)
- Trigonométrie (s’ouvrira dans une nouvelle fenêtre)
Les liens vers ces vidéos sont uniquement fournis à titre de suggestion. On t'encourage à trouver d'autres ressources pour parfaire ta compréhension.
Il existe trois méthodes pour l’addition (et la soustraction) des vecteurs :
- Méthode 1 : Les dessins à l’échelle
- Méthode 2 : L’algèbre (la trigonométrie : les lois des sinus et des cosinus)
- Méthode 3 : Les composantes perpendiculaires du vecteur
Bien que cette activité d’apprentissage soit consacrée aux vecteurs de mouvement (comme le déplacement, la vélocité et l'accélération), tu auras également à appliquer les concepts relatifs aux vecteurs tout au long de ce cours. Savoir dessiner et représenter un vecteur constitue une compétence essentielle pour ce cours de physique. Voyons maintenant comment appliquer cette compétence.
Méthode 1 : L’addition vectorielle au moyen de dessins à l’échelle
Pour additionner des vecteurs, on dessine le premier, puis on place la « queue » du vecteur suivant contre la « tête » ou « pointe » du premier. C’est ce qu’on appelle la méthode de la tête à la queue.
On trouve le vecteur résultant en reliant la « queue » du premier vecteur à la « tête » ou « pointe » du dernier vecteur. Autrement dit, pour déterminer le déplacement résultant en additionnant deux vecteurs de déplacement, il faut relier la position « Départ » à la position « Fin » avec un vecteur.
Tu doutes encore de savoir appliquer cette méthode? Regarde cette vidéo de la série Les vecteurs à deux dimensions : introduction (s’ouvrira dans une nouvelle fenêtre).
Le lien vers cette vidéo est uniquement fourni à titre de suggestion. On t'encourage à trouver d'autres ressources pour parfaire ta compréhension.
À visionner
Sers-toi de tes connaissances sur l'addition des vecteurs et tente de résoudre les exemples suivants dans ton carnet de notes avant de révéler la solution pour chaque situation.
Exemple 1 :
Voici Ryan. Il écoute sa liste de reproduction favorite en allant rejoindre quelques amis.
Calcule le déplacement qu’il effectue s’il marche 14 m [N], puis 25 m [S].
Solution :
Dans un diagramme vectoriel, dessine les deux vecteurs de déplacement, puis le vecteur résultant.
et

La queue du vecteur 2 a été placée à côté de la tête du vecteur 1. On détermine le déplacement résultant (ou total) en reliant la position « départ » à la position « fin » à l'aide d'un vecteur. Il faut dessiner des pointes de flèches sur les vecteurs pour indiquer leur direction.
Qu’arrive-t-il cependant quand les vecteurs ne sont pas alignés dans une même dimension?
Exemple 2 :
Félicie est en route pour rencontrer Ryan, mais elle est à l'autre bout de la ville. Elle marche 25 m [est], puis 30 m [nord]. Détermine quel est son déplacement.
Autovérification
Mettons maintenant à l’épreuve tes connaissances sur les sujets que nous avons vus jusqu’ici avant de passer aux méthodes 2 et 3.
Il faut suivre un ordre précis quand on dessine un diagramme à l'échelle pour résoudre un problème de déplacement. Quel est cet ordre?
À l'aide des menus déroulants, place les étapes dans le bon ordre pour déterminer le déplacement.
Carnet de notes
Prêt pour un autre exemple?
Sers-toi de ta règle et de ton rapporteur d’angle pour dessiner un diagramme vectoriel afin de résoudre le problème suivant.

Un camion portant une pleine cargaison d'ordinateurs en Ontario parcourt 45 km vers l’ouest, puis 65 km vers le sud.
Calcule le déplacement du camion.
79 km [ouest 55° sud]
Voici ce à quoi devrait ressembler ton schéma :

Avec une échelle de 1 cm = 10 km, en mesurant le vecteur de déplacement, tu devrais constater qu'il a une longueur d’environ 7,9 cm. En mesurant l’angle θ, tu devrais constater qu’il est d’environ 55° de l’ouest vers le sud.
Un diagramme à l'échelle peut parfois donner un résultat légèrement différent de la bonne réponse, car il est difficile de tout mesurer avec précision.
Pour trouver la réponse de façon plus précise, on peut utiliser l'algèbre au lieu de dessins à l'échelle. C'est ce que nous allons apprendre maintenant. → Méthode 2 : L’addition de vecteurs au moyen de l’algèbre
Méthode 2 : L’addition de vecteurs au moyen de l’algèbre
Il peut t’être utile de réviser les concepts de base de la trigonométrie pour mieux comprendre cette méthode.
Revenons sur les quelques premiers exemples de cette leçon. Cette fois-ci, nous résoudrons les problèmes grâce à l’algèbre au lieu de dessins à l’échelle. La réponse devrait être la même :
Exemple 1 : Tu te souviens de Ryan? Calcule le déplacement qu’il effectue s’il marche 14 m [N], puis 25 m [S].
Solution : L’addition de vecteurs au moyen de l’algèbre
En utilisant l'algèbre, calcule et
Remarque : Il faut que les vecteurs aient la même direction pour qu’on puisse les additionner algébriquement.
Ryan s’est déplacé de 11 m vers le sud.
Exemple 2
Tu te souviens de Félicie? Elle marche 25 m [est], puis 30,0 m [nord]. Détermine son déplacement.
Solution : L’addition de vecteurs au moyen de l’algèbre
Il te faudra quand même dessiner un diagramme, mais il peut s'agir d'un croquis rapide au lieu d'un dessin à l'échelle.

Applique le théorème de Pythagore pour trouver la grandeur du déplacement résultant. . Rappelle-toi que constitue l’hypoténuse (le côté c), alors que les deux autres côtés sont a et b.
Utilise la trigonométrie pour calculer l’angle. Le vecteur de 30 m est le côté opposé, et celui de 25 m est le côté adjacent.
Pour trouver la réponse finale, il faut combiner l'angle et la grandeur du déplacement :
Félicie s’est déplacée de 39 m [est 50° nord]. Consulte la réponse que tu as calculée au moyen des dessins à l'échelle; tu devrais avoir obtenu la même.
Carnet de notes
Refais l'exemple de l’autovérification, cette fois en utilisant la méthode 2, l'algèbre, au lieu d'un dessin à l'échelle. Crois-tu que tu obtiendras le même réponse qu’avec la méthode 1? Il n’y a qu’une façon de le savoir.
Un camion portant une pleine cargaison d'ordinateurs parcourt 45 km [ouest], puis 65 km [sud]. Calcule le déplacement du camion.

Étape 1 : Trouver l’hypoténuse.

Applique le théorème de Pythagore pour calculer .
Rappelle-toi que constitue l’hypoténuse (le côté c), alors que les deux autres côtés sont a et b.
Étape 2 : Trouver la mesure de l’angle.
Utilise la trigonométrie pour calculer l’angle. Le vecteur de 65 km est le côté opposé, et celui de 45 km est le côté adjacent.
Étape 3 : Combiner l'angle et la grandeur du déplacement.
Pour trouver la réponse finale, il faut combiner l'angle et la grandeur du déplacement :
Le déplacement du camion est de 79 km [ouest 55° sud].
Consulte la réponse que tu as calculée au moyen des dessins à l'échelle (méthode 1); tu devrais avoir obtenu la même.
L’addition de vecteurs (sans triangle rectangle)
Jusqu'ici, nous avons vu comment additionner des vecteurs qui forment un triangle rectangle. Comment peut-on maintenant additionner des vecteurs qui ne forment pas un triangle rectangle?
Le prochain exemple te montrera comment y parvenir.
Exemple
Un tramway de Toronto traversant la ville. Calcule le déplacement d'un wagon porte-conteneurs qui parcourt 80,0 km [N], puis 1,0 x 10² km [O 20° N].
Servons-nous des trois différentes méthodes que nous avons apprises pour résoudre ce type de problème.

Méthode 1 : Les dessins à l’échelle
Pour résoudre ce problème, il te faut choisir une échelle adéquate.
Dans ce cas-ci, une échelle adéquate en serait une de 1 cm = 10 km; donc, 80 km = 8 cm et 100 km = 10 cm.
Étape 1 : effectuée.
Étape 2 : Dessine les deux vecteurs de déplacement en les reliant de la pointe à la queue.
Méthode 1 : Étape 7
Applique l'échelle pour changer la longueur mesurée de la résultante en un vecteur, puis donne la réponse finale avec la direction.
14,7 cm x 10 km = 147 km
Sers-toi d’un rapporteur pour mesurer l'angle (la direction).
Le déplacement du wagon porte-conteneurs est de 147 km [N 41° O].
Méthode 2 : La trigonométrie (les lois des sinus et des cosinus)
Algébriquement, lorsqu’on additionne des vecteurs comme dans l'exemple ci-dessus, on peut appliquer les lois des sinus et des cosinus pour calculer le vecteur résultant. Voici le même exemple :
Calcule le déplacement d'un wagon porte-conteneurs qui parcourt 80,0 km [N], puis 1,0 x 10² km [O 20° N].
Voici comment le résoudre avec du papier et un crayon.
Trouve la grandeur.
Trouve la direction.

Le déplacement du wagon est donc de 148 km [N 39° O].
Comparativement aux dessins à l'échelle, cette méthode de résolution permet d'obtenir un vecteur résultant plus précis.
C'est pour ça que la valeur donnée par les dessins à l’échelle est légèrement différente de la réponse obtenue avec cette méthode-ci.
Méthode 3 : Les composantes perpendiculaires du vecteur
La troisième méthode d'addition de deux ou plusieurs vecteurs est basée sur la résolution ou la déconstruction d'un vecteur en ses composantes perpendiculaires.
Il s'agit d'une procédure très courante. Examinons-la de près pour nous assurer que tu comprends bien comment l’appliquer.
Tout vecteur peut être représenté en deux dimensions comme ayant des sections qui se trouvent le long de l'axe des x et d’autres le long de l'axe des y.
Par exemple, un vecteur de déplacement de 5,0 m [N 45° E] aura une composante qui est parallèle à l'axe des x et une autre parallèle à l'axe des y. Ces composantes sont perpendiculaires les unes par rapport aux autres.
![Vecteur indiquant un déplacement de 5,0 m [N 45° E].](../assets/img/sph4u_01.01.43.svg)
Pour résoudre le vecteur en ses composantes perpendiculaires, tu dois faire appel aux rapports trigonométriques :
Pour additionner des vecteurs en deux dimensions, tu dois d’abord résoudre (ou décomposer) tous les vecteurs en leurs composantes perpendiculaires, puis additionner toutes les composantes parallèles.
Une fois que tu l'auras fait, tu peux employer le théorème de Pythagore et la tangente afin de déterminer la grandeur du vecteur résultant et sa direction (angle).
Voici le même exemple que précédemment, mais résolu par la méthode des composantes :
Calcule le déplacement d'un wagon porte-conteneurs qui parcourt 80,0 km [N], puis 1,0 x 10² km [O 20° N].
[Nord] et [est] sont les directions positives.
Le déplacement du wagon est donc de 148 km [N 39° O].
Tu remarqueras que la réponse est LA MÊME qu’avec la méthode précédente.
Si tu dois additionner plus de deux vecteurs, suis ces mêmes étapes, mais après avoir tracé le deuxième vecteur, dessine un nouvel ensemble de coordonnées à la tête du deuxième vecteur et trace le troisième vecteur à partir de là.
Rappelle-toi que la résultante correspond à la droite tracée entre l’origine (la queue) du premier vecteur et l’extrémité (la tête) du dernier.
Cette vidéo montre comment tracer l'addition de trois vecteurs.
Exercice
C’est en répétant qu’on maîtrise la matière. Assurons-nous que tu es à l'aise avec toutes les équations enseignées dans cette leçon. Pour ces exercices, il te faudra ton carnet de notes, une règle et un rapporteur d’angle.
Utilise le tableau ci-dessus pour décider si tu dois employer la méthode algébrique ou les dessins à l'échelle.
1. Quelqu’un parcourt 8,0 km [N], 6,0 km [O] en voiture. Détermine son déplacement total au moyen du théorème de Pythagore et de la trigonométrie.
Solution : Avec le théorème de Pythagore.
Éléments connus :
Inconnue :
Analyse et solution :
Le déplacement résultant est de 1,0 x 10¹ km [N 37° O].
2. Une personne avance de 2,0 m [E 20° S] à pied, puis de 4,0 m [S]. Détermine son déplacement total au moyen de la trigonométrie (lois des sinus et des cosinus).
Solution : À l’aide des lois des sinus et des cosinus.
![Vecteur indiquant un déplacement de 5,0 m [N 45° E].](../assets/img/sph4u_01.01.45.svg)
D’après le diagramme ci-dessus, on ajoute 20° pour obtenir 68°.
Le déplacement résultant est de 5,0 m [E 68° S] ou [S 22° E]
3. Un camion parcourt 1,0 x 102 km [S], tourne et roule sur 80,0 km [O 30° S], puis tourne à nouveau et fait 20,0 km [N] de plus. Calcule son déplacement total au moyen de la méthode des composantes perpendiculaires.
Solution : Avec la méthode des composantes perpendiculaires.
Les directions [nord] et [ouest] sont positives.
Le déplacement résultant est de 139 km [S 30° O].
Autovérification
C'est de nouveau le moment de sortir ton carnet de notes et d'essayer de résoudre toi-même les questions suivantes. Compare ensuite tes réponses aux réponses suggérées.
- Résous les vecteurs suivants en leurs composantes.
- 17 m/s [N]
- 40 m/s [S 45° E]
Exercice
Carnet de notes
Résous les vecteurs suivants en leurs composantes.
1. Résous ce vecteur en ses composantes.
25 m/s [E]
Comme il n’y a pas de composante verticale, ce vecteur reste tel quel.
2. Résous ce vecteur en ses composantes.
95 m/s [N 20° O]
L’addition de vecteurs au moyen des composantes
Voir « Addition de vecteurs au moyen des composantes »(s’ouvrira dans une nouvelle fenêtre) pour en savoir plus sur l'ajout de vecteurs à l'aid de composants.
Autovérification : L’addition des vecteurs
Carnet de notes
On peut additionner deux vecteurs uniquement si leurs unités et leurs directions sont les mêmes. Que doit-on faire si leur direction est :
a) colinéaire (c.-à-d. sur la même ligne), mais en direction opposée?
Si deux vecteurs sont colinéaires, mais de direction opposée, il faut rendre leur direction identique. Pour ce faire, on convertit un des vecteurs en une grandeur négative (valeur scalaire) ayant la même direction que l'autre vecteur.
Par exemple :
Si le vecteur n° 1 avait une direction [E] et le vecteur n° 2 une direction [O], alors la direction du vecteur n° 1 pourrait être convertie de [E] en -[O].
(La valeur négative de la direction est égale à la valeur positive d'une direction à 180° de son orientation initiale.)
b) non colinéaire (c.-à-d. sur des lignes différentes)?
Quand on a deux vecteurs non colinéaires, il faut les additionner, de la tête à la queue, et dessiner le vecteur résultant (en partant de la queue du premier vecteur et en terminant à la tête du dernier vecteur). On doit ensuite décider comment résoudre le problème mathématiquement.
Si le diagramme produit un triangle rectangle, on peut se servir du théorème de Pythagore et des fonctions trigonométriques pour calculer la grandeur et la direction du vecteur.
Si le triangle n’est pas rectangle, on peut
- Résoudre chaque vecteur en ses composantes x et y;
- Additionner les composantes x entre elles;
- Additionner les composantes y entre elles;
- Additionner les résultats des deux opérations précédentes pour obtenir un triangle rectangle qui montre le vecteur résultant.
- Ensuite, appliquer le théorème de Pythagore pour trouver la grandeur du vecteur résultant.
- On peut employer la fonction inverse de la fonction tangente pour calculer l’angle.
OU
On peut créer le triangle formé par les vecteurs et utiliser une combinaison des lois des sinus et des cosinus. Il peut s’avérer nécessaire d’utiliser la géométrie pour ramener l'angle dans un cadre de référence standard (N-S-E-O).
Partie 1 : Résume ce que tu as appris.
Tu as étudié les vecteurs en profondeur et tu les as appliqués à toute une série de nouveaux scénarios. Tu continueras de travailler avec les vecteurs alors que nous poursuivons notre étude du mouvement dans ce cours.
Carnet de notes
Recopie le tableau suivant dans ton carnet de notes. Pour t’aider à consolider ta compréhension des vecteurs, remplis le tableau des vecteurs. Compare ensuite tes réponses à celles que tu vois à l’écran.
Partie 2 : Création d’un organigramme conceptuel
Un organigramme conceptuel est une sorte d’organisateur graphique. Il commence par une idée ou un concept principal, auquel se rattachent des sous-thèmes et les concepts connexes. Commence par une idée, une question ou un sujet central, puis trouve les concepts-clés qui s’y rattachent.
Trouve les concepts-clés directement reliés au sujet principal. Ainsi, un organigramme conceptuel est un organisateur graphique hiérarchisé où un ordre de priorité est donné aux différents sujets/concepts. Trouve les autres concepts rattachés aux concepts-clés et ajoute à l’organigramme autant de branches qu’il le faut.
La caractéristique particulière de l’organigramme conceptuel est qu’il permet de relier entre eux les concepts ou les termes grâce à des mots et des énoncés de liaison. C’est ce qui distingue un organigramme conceptuel d’un arbre conceptuel. Il est possible d’établir des liens entre deux concepts, et des réseaux peuvent être créés lorsque des liens sont établis avec d’autres zones de l’organigramme. L’établissement de liens entre les concepts joue un rôle important dans la compréhension des sujets complexes.
Un organigramme conceptuel commence par une idée ou un concept principal auquel se rattachent des sous-thèmes et des concepts connexes. Commence par une idée, une question ou un sujet central, puis trouve les concepts-clés qui s’y rattachent.
Trouve les concepts-clés directement reliés au sujet principal. Un organigramme conceptuel est donc un organisateur graphique hiérarchisé où un ordre de priorité est donné aux différents sujets et concepts. Tu peux trouver les autres concepts rattachés aux concepts-clés et ajouter à l’organigramme autant de branches qu’il le faut.
La caractéristique particulière de l’organigramme conceptuel est qu’il permet de relier entre eux les concepts ou les termes grâce à des mots et des énoncés de liaison. C’est ce qui distingue un organigramme conceptuel d’un arbre conceptuel. Il est possible d’établir des liens entre deux concepts, et des réseaux peuvent être créés lorsque des liens sont établis avec d’autres zones de l’organigramme. L’établissement de liens entre les concepts joue un rôle important dans la compréhension des sujets complexes.
Comment élabore-t-on un organigramme conceptuel?
Sers-toi d’un organigramme conceptuel pour ordonner les termes en fonction de leurs relations entre eux après chaque activité d'apprentissage. À la fin de chaque unité, tu combineras tes organigrammes conceptuels pour produire ainsi un organisateur graphique complet résumant les concepts clés de l'unité.
Tu peux créer tes organigrammes conceptuels à la main OU par ordinateur.
Tu doutes encore de savoir comment créer un organigramme conceptuel?
À visionner
Regarde la vidéo d’explication suivante pour en apprendre davantage en étudiant un exemple étape par étape. « Comment créer un organigramme conceptuel » (s’ouvrira dans une nouvelle fenêtre)
Tu devras créer un organigramme conceptuel après chaque activité d’apprentissage.
Le lien vers cette vidéo est uniquement fourni à titre de suggestion. On t'encourage à trouver d'autres ressources pour parfaire ta compréhension.
À la fin de chaque unité, tu combineras tes organigrammes conceptuels pour produire ainsi un organisateur graphique complet résumant les concepts de l'unité.
À la fin de chaque unité, tu soumettras ton organisateur graphique à ton enseignant ou enseignante en vue d’obtenir sa rétroaction à son sujet (mais pas de note). À la fin du cours, tu organiseras tous tes organigrammes conceptuels ou tu les combineras en un seul grand organigramme complet à soumettre pour qu’il soit noté.
SPH4U - Activité finale (organigrammes conceptuels)
Tu as élaboré un organigramme conceptuel pour chacune des quatre premières unités de ce cours. C’est maintenant le temps d’en créer un pour l’Unité 5 (La physique moderne). Une fois que tu auras terminé ton organigramme conceptuel pour l’Unité 5, tu devras rassembler les organigrammes que tu as préparés pour chacune des unités du cours.
Instructions à l’apprenant ou l’apprenante :
- Tu devras décider si tu prépares ton organigramme conceptuel pour l'ensemble du cours à l’ordinateur ou à la main.
- Cet organigramme sera assez grand et complexe, alors assure-toi de laisser suffisamment de place pour chacune des cinq unités.
- Ton sujet ou concept principal sera « LA PHYSIQUE ». Tu créeras ensuite des ramifications afin d’y relier les autres concepts.
- Relie les concepts par des flèches et des titres si tu dois établir des liens entre les diverses unités. Remarque : Il n’est pas nécessaire que les flèches soient droites; elles peuvent être courbées.
Exemple d’organigramme conceptuel

Grille d'évaluation de l’organigramme conceptuel d’ensemble
Évaluation : Ton travail sera évalué en fonction de la grille d’évaluation suivante. Assure-toi de bien lire cette grille avant de rédiger ton travail et de le soumettre en vue d’une notation. Étudie cette grille d’évaluation expliquée (s’ouvrira dans une nouvelle fenêtre) pour mieux comprendre les catégories ou les niveaux.
Évaluation : Ton travail sera évalué en fonction de la grille d’évaluation suivante. Assure-toi de bien lire cette grille avant de rédiger ton travail et de le soumettre en vue d’une notation. Étudie cette grille.
L’introduction du cours comprenait des idées sur la façon de construire des organigrammes conceptuels. Choisis la manière dont tu veux créer tes organigrammes et commence dès maintenant en en élaborant un premier. Quand tu as terminé, mets-le de côté pour t’en servir de nouveau à la fin de l’unité.
Concepts à inclure : (plus d’une fois si nécessaire)
- Le mouvement
- Les vecteurs
- Les quantités scalaires
- Le mouvement uniforme
- Le mouvement non uniforme
- La grandeur
- La direction
- La distance
- Les composantes
- L’addition des vecteurs
- La soustraction des vecteurs
- La géométrie
- Les dessins à l’échelle
Partie 3 : Réflexion sur ton apprentissage
Carnet de notes
Tu as appris trois méthodes différentes d’addition des vecteurs.
Chacune de ces méthodes a ses avantages et ses inconvénients. À l’aide de ce que tu as appris et constaté en appliquant ces différentes méthodes, reproduis pour chaque méthode les tableaux à deux colonnes ci-dessous dans ton cahier de notes et remplis-les.
| Méthode 1 : Les dessins à l’échelle | |
|---|---|
| Avantages | Inconvénients |
| Méthode 2 : La trigonométrie | |
|---|---|
| Avantages | Inconvénients |
| Méthode 3 : Les composantes perpendiculaires | |
|---|---|
| Avantages | Inconvénients |
Pour en savoir plus
C’est en répétant qu’on maîtrise la matière.
Lance le simulateur ci-dessous pour appliquer et renforcer toutes tes connaissances sur les vecteurs :















![Un vecteur de 17 m/s [nord] est représenté sur un axe nord-est.](../assets/img/sph4u_01.01.49.svg)



